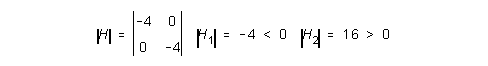
H05 Voiton maksimointi
1. Jos esimerkin 1 yrityksen kustannusfunktio on
C = 2 Q12 + 2 Q22
a) Ovatko näiden kahden hyödykkeen tuotannot vieläkin teknisessä riippuvuussuhteessa toisistaan?
Vastaus:
Eivät ole, koska kummankin tuotannon rajakustannukset ovat riippumattomat toisen tuotannon määrästä.
b) Mitkä ovat optimituotannon määrät Q1 ja Q2?
Vastaus:
Voittofunktio:
TP = P10 Q1 + P20 Q2 - 2 Q12 - 2 Q22
Ensimmäisen kertaluvun ehto:
TP1 = P10 - 4 Q1 = 0 TP2 = P20 - 4 Q2 = 0
Q1 = P10/4 Q2 = P20/4
Hesse
TP11 = -4, TP12 = TP21 = 0, TP22 = -4
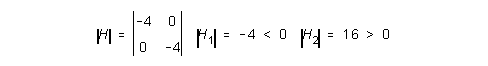
siis maksimi
c) Mikä on TP12 arvo? Mikä on sen talousteoreettinen tulkinta?
Vastaus:
TP12 = 0 kummankin hyödykkeen tuotanto on voiton maksimissa riippumaton toisen tuotannon määrästä.
Tuotanto tapahtuu ikäänkuin kysymyksessä olisi kaksi tehdasta, jotka tuottavat eri tuotteita ja optimoivat tuotantonsa toisesta riippumatta.
2. Jos esimerkin 2 kysyntäfunktiot ovat
Q1 = 40 - 2 P1 - P2
Q2 = 35 - P1 - P2
ovatko hyödykkeet kulutuksen suhteen toisistaan riippuvaisia? Miten se näkyy?
Vastaus:
Kyllä. Hyödykkeet täydentävät toisiaan. Jos toisen hinta nousee, sekä tämän hyödykkeen että sitä täydentävän hyödykkeen kysyntä supistuu.
3. Kaksituoteyrityksellä on edellisen harjoituksen kysyntäfunktiot ja kustannusfunktio
C = Q12 + 2 Q22 + 10
a) Etsi maksivoiton antavat kaksi tuotannon arvoa, jotka toteuttavat ensimmäisen kertaluvun ehdon.
Vastaus:
Keskituotto (=hinta) P = P(Q)
2 P1 + P2 = 40 - Q1
P1 + P2 = 35 - Q2
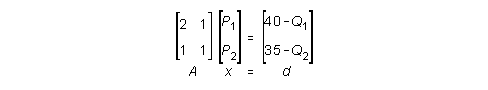
Cramer:
DET = 2(1) - 1(1) = 1
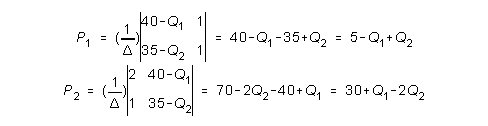
Kokonaistuotto:
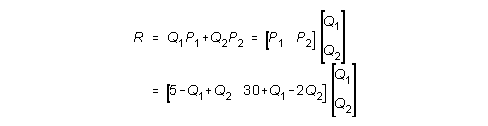
R = 5 Q1 - Q12 + Q1 Q2 + 30 Q2 + Q1 Q2 - 2 Q22
R = 5 Q1 - Q12 + 2 Q1 Q2 + 30 Q2 - 2 Q22
Voitto = Tuotto - Kustannukset
TP = R - C
= 5 Q1 - Q12 + 2 Q1 Q2 + 30 Q2 - 2 Q22 - Q12 - 2 Q22 - 10
= 5 Q1 - 2 Q12 + 2 Q1 Q2 + 30 Q2 - 4 Q22 - 10
Ensimmäisen kertaluvun (=välttämätön) ehto: 1 derivaatat nolliksi
TP1 = 5 - 4 Q1 + 2 Q2 = 0
TP2 = 30 + 2 Q1 - 8 Q2
= 15 + Q1 - 4 Q2 = 0
Järjestetään matriisioperaatioita varten
- 4 Q1 + 2 Q2 = - 5
Q1 - 4 Q2 = - 15
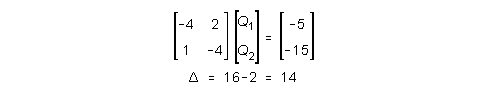
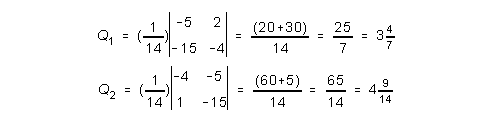
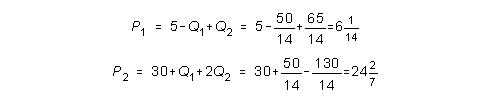
b) Tarkista, että myös toisen kertaluvun ehto on täytetty.
Vastaus:
Riittävä ehto: 2 derivaatat ja Hesse
TP11 = - 4 TP12 = TP21 = 2 TP22 = - 8
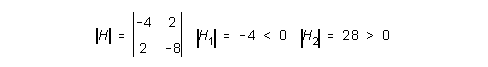
siis maksimi
c) Mikä on voiton maksimi?
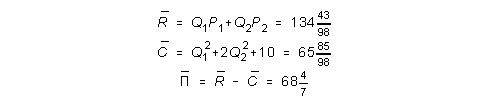
Kansantalouden kurssit o AJK kotisivu
Asko Korpela, kansantaloustieteen lehtori, Helsingin kauppakorkeakoulu
Asko.Korpela@kolumbus.fi (palaute Asko Korpelalle) o salo@hkkk.fi (palaute Seppo Salolle)
Asko Korpela 970930 (970930)
[ccc]