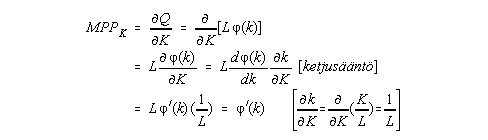
H08 Tuotantofunktio ja kustannusminimi

1. Osoita kohtien a)-d) paikkansapitävyys lauseiden (12.46) ja (12.50) perusteella olettaen, että skaalatuotot ovat vakio.

a) APP_L voidaan piirtää riippumattomana muuttujana k (= K/L) akseliin nähden.

Vastaus: OM1 s. 2 (12.46)

APP_L = (k) (= Q/L)

Tässä siis: argumentti on k ja funktio on APP_L.

b) MPP_K voidaan ilmaista APP_L käyrän kulmakertoimena.

Vastaus: OM2 s. 2 (12.50)

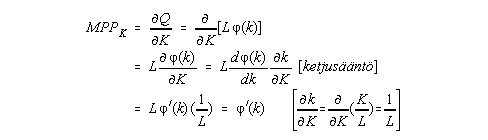
c) APP_K voidaan ilmaista APP_L käyrän kulmakertoimena.

Vastaus: OM1 s. 2 (12.46)

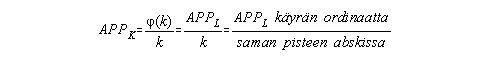
d) MPP_K = APP_L - k(MPP_K) = APP_L - k(APP_L kulmakerroin).

Vastaus: OM2 s. 2 (12.49)

MPP_L = (k) - k'(k) = APP_L - k MPP_K

2. Oletetaan Q = AK L. Osoita, että

a) + > 1 merkitsee suurtuotannon etuja (= kasvavia skaalatuottoja).

Vastaus:

Jos + > 1, suurtuotannon edut ovat voimassa, koska funktion arvo enemmän kuin k-kertaistuu, jos L ja K kerrotaan luvulla k.

b) + < 1 merkitsee alenevia skaalatuottoja.

Vastaus:

Jos + < 1, alenevat skaalatuotot samasta syystä kuin edellä.

ESIM.

K = 2 L = 3 A = 1 k = 2

a) = 0.3 = 0.8 => = 1.1

Q₀ = 2^0.3 3^0.8 =

Q₁ = (2x2)^0.3 (2x3)^0.8 = = 2^1.1 Q₀ (2^1.1 > 2 )

b) = 0.3 = 0.6 => = 0.9

Q₀ = 2^0.3 3^0.6 =

Q₁ = (2x2)^0.3 (2x3)^0.6 = = 2^0.9 Q₀ (2^0.9 < 2)

3. Jos Cobb-Douglas tuotantofunktiossa suhde / esitetään suhteen P_a/P_b funktiona (piirrä käyrä), millainen kuvio saadaan? Riippuuko tulos olettamuksesta + = 1? Miten tästä käyrästä luetaan korvausjousto?

Vastaus:

Koska (/) = (/) (P_a/P_b), kuvio on suora, joka kulkee origon kautta. Ei riipu siitä, onko + = 1. Korvausjousto on tämän suoran jousto. Origon kautta kulkevan suoran jousto on aina E = 1.

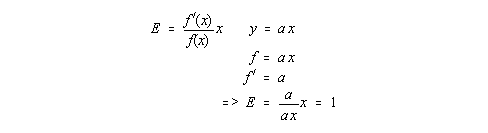
4. Mitä merkitsee samakustannussuorien samansuuntaisuus?

Vastaus:

Rahankäytön lisäystä, hintasuhde säilyy ennallaan.

Kansantalouden kurssit   o  AJK kotisivu

Asko Korpela, kansantaloustieteen lehtori, Helsingin kauppakorkeakoulu

Asko.Korpela@kolumbus.fi  (palaute Asko Korpelalle) o salo@hkkk.fi  (palaute Seppo Salolle)

Asko Korpela 970930 (970930)

[ccc]