Asko Korpela: Kansantalouden
peruskurssi:
Osa 2 KOTITALOUS JA YRITYS
(Asko.Korpela@kolumbus.fi) o Sisällysluettelo
o AJK kurssit o AJK
kotisivu
3.1 Kulutus ja käytettävissä
oleva tulo
o Tulot, kulutus ja säästäminen
o Kotitalouden kulutusfunktio
o Kulutus ja säästäminen
o Kulutus ja perheen koko
3.2 Kotitalouden tasapainoteoria
o Budjettisuora
o Rajahyötyteoria
Yhteenveto: Kuluttajan käyttäytyminen
Taulukot:
T3.1 Tulot, kulutus
ja säästäminen
T3.2 Lisätulon vaikutus
kulutukseen
T3.3 Kokonaishyöty ja rajahyöty
Kuviot
K3.1 Kulutuksen riippuvuus
tuloista
K3.2 Kotitalouden kulutusfunktio
K3.3 Budjettisuora ja tulovaikutus
K3.4 Budjettisuora ja hintavaikutus
K3.5 Kokonaishyöty
K3.6 Rajahyöty
Kahdessa ensimmäisessä luvussa tarkasteltiin kansantalouden rakennetta yleisesti sekä erityisesti Suomen kansantaloutta. Päätarkoituksena oli mieltää keskeisiä kansantalouden osien suuruussuhteita ja muodostaa konkreettinen kokonaiskuva siitä havaintoaineistosta, jota taloustieteessä tutkitaan.
Nyt olemme valmiit siirtymään rakenneanalyysista vaikutusanalyysiin eli taloudelliseten ilmiöiden syiden ja seurausten selvittelyyn. Tässä kirjan toisessa osassa pysytään koko ajan mikrotasolla eli tarkastellaan yhtä päätöksentekijää: kuluttajaa ja yrittäjää. Kolmannessa osassa asioita tarkastellaan makrotasolla eli koko kansantalouden kannalta. Neljännessä osassa mielenkiinnon kohteena on talouspolitiikka eli kansantalouden ohjaaminen haluttuun suuntaan.
Edellä todettiin, että kotitaloudet tekevät kulutuspäätöksensä tulojen asettamissa rajoissa hyötyä ja hintaa vertaamalla. Tavallaan siis kulutuspäätös on kaksiosainen: kulutustaso määräytyy tulojen mukaan, mutta yksittäisen hyödykkeen ostopäätöstä tehtäessä valinta tapahtuu lähinnä eri vaihtoehtojen hintojen perusteella.
Ensiksi tarkastelemme tulojen vaikutusta kulutukseen eli kulutusfunktiota empiirisen havaintoaineiston perusteella ja sen jälkeen kohdassa 3.2 kuluttajan tasapainoteoriaa esimerkkien avulla.
Tuskin on mahdollista löytää kahta perhettä, jotka käyttäisivät tulonsa täsmälleen samalla tavalla, vaikka tulot olisivatkin yhtä suuret. Perheen koko, lasten ikä, se, asuuko perhe maalla vai kaupungissa, ovat asioita, jotka suuresti vaikuttavat siihen, mitä hyödykkeitä ja paljonko perheessä kulutetaan.
On luonnollista, että perheessä, jossa kuukausitulot ovat 10000 mk kulutetaan suhteellisesti paljon suurempi osa tuloista ruokaan ja asuntoon kuin perheessä, jonka kuukausitulot ovat esim. 25000 mk.
Mitä korkeammalla tulotasolla perhe on, sitä pienempi on elintarvikkeiden ja muiden välttämättömyys-hyödykkeiden osuus kulutusmenoista.
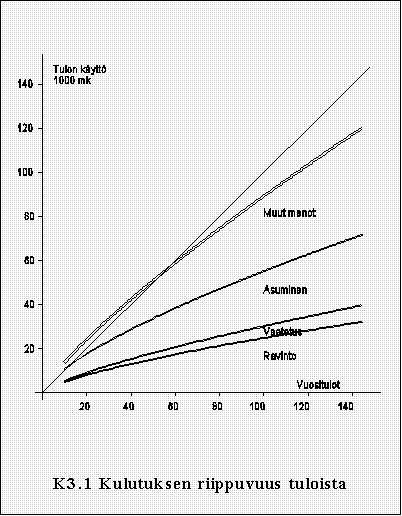
Tämän jokapäiväisestä elämästä saatujen kokemusten perusteella ymmärrettävän väitteen, joka tunnetaan nimellä Engelin laki, ovat useat tutkimukset osoittaneet todeksi. Toinen kulutusta koskeva perustotuus, joka myös käy selville kuviosta K3.1 on:
Mitä korkeammalla tulotasolla perhe on, sitä pienempi osuus tuloista menee kulutukseen.
Jos tutkitaan esim. 1000 sattumanvaraisesti valitun perheen kirjanpitoa ja asetetaan nämä perheet tulojen mukaiseen järjestykseen, havaitaan, että alimmassa tuloluokassa tuskin voidaan lainkaan säästää, päinvastoin: saatetaan joutua turvautumaan entisiin säästöihin tai joudutaan velkaantumaan. Korkeimmissa tuloluokissa tuloista riittää osa säästöön. Tässä mielessä säästäminen on täysin verrattavissa elintasohyödykkeisiin. Tulon käyttö kulutukseen vähenee ja käyttö säästämiseen lisääntyy sitä nopeammin, mitä korkeammalle tulotasolle tullaan.
Kuvio K3.1 esittää kulutuksen ja säästämisen riippuvuutta perheen kokonaismenoista. Tämä kuvio perustuu Tilastokeskuksen vuonna 1985 suorittamaan laajaan, lähes 9000 kotitaloutta kaikissa väestöryhmissä maaseudulla ja kaupungeissa käsittäneeseen tutkimukseen. Sen mukaan perheen keskimääräinen henkilöluku oli vuonna 1985 2.36. Tulonsaajia oli perheessä 1.15. Perheen keskimääräinen käytettävissä oleva vuositulo oli tämän tutkimuksen mukaan 84 400 mk (= 35 800 mk henkeä kohti). Tästä kulutukseen käytettiin 77 400 mk (32 800 mk) ja säästämiseen 7000 mk (3000 mk).

Tämän tutkimuksen tulokset ovat hyvin sopusoinnussa eri puolilla maailmaa suoritettujen vastaavien tutkimusten kanssa. Näiden tutkimusten perusteella on voitu todeta että tulojen kasvaessa perheen:
1. ravintomenot kasvavat hitaammin kuin perheen tulot tai kokonaismenot. Suomessa tämän tutkimuksen mukaan 10% kokonaismenojen kasvua vastaa keskimäärin 8.6% kasvu ravintomenoissa, jotka käsittävät ruoan, juomat ja tupakan.
2. vaatetusmenot kasvavat sen sijaan hiukan nopeammin kuin kokonais-menot. Suomessa 10% kokonaismenojen kasvua vastaa 11.5% suuruinen kasvu vaatetus- ja jalkinemenoissa.
3. asumiseen liittyvät menot kasvavat myös selvästi hitaammin kuin koko-naismenot. Suomessa 10% menojen kasvua vastaa 8.2% lisäys asuntoon, valoon ja lämpöön sekä kotitalouskalustoon uhrattavissa menoissa.
4. muut menot sensijaan kasvavat selvästi nopeammin kuin kokonaismenot. Vuoden 1985 havaintoaineiston mukaan 10% kokonaismenojen kasvua vastaa 12.2% kasvu muissa menoissa eli henkilökohtaiseen puhtauteen, terveyden- ja sairaudenhoitoon, liikenteeseen, virkistäytymiseen, huvitteluun ja koulutukseen ym. käytettävissä menoissa.
Muistaen kulutuskysynnän ratkaisevan merkityksen kansantalouden liikkeelle panevana voimana pyrimme edelleen syventämään tietoamme kulutuksen tasoon vaikuttavista tekijöistä. Yksinkertaisuuden vuoksi emme enää kiinnitä huomiota kulutuksen osatekijöihin vaan kulutukseen ja säästämiseen koko-naisuuksina. Kuviosta K3.1 saimme karkean käsityksen kulutuksen ja säästämisen suhteista. Asia käy selvemmäksi, kun tarkastelemme taulukkoa T3.1, jonka perusteella kuvio on piirretty. Tässä taulukossa kulutus on jaettu tulojen suuruuden mukaan desiileihin eli kymmenen luokkaan.

Kuviosta ja taulukosta nähdään, että alimmilla tulotasoilla tulot eivät riitä, vaan osa kulutuksesta on avustusten, entisten säästöjen ja lainojen varassa. Siirryttäessä ylemmille tulotasoille tulot riittävät yhä paremmin. Tietyllä tasolla, jossakin 50 tuhanneen markan vaiheilla, tulot juuri riittävät kulutukseen. Tulojen noustessa tämän tason yli perheellä on keskimäärin mahdollisuus myös säästämiseen. Mitä suuremmat tulot, sitä suurempi osuus niistä liikenee säästöön ja sitä pienempi osuus tarvitaan kulutukseen. Tulotasolla 70 000 mk säästämisen osuus on 2 % ja kulutuksen 98 %, kun sen sijaan ylimmässä desiilissä säästöön voidaan panna 19 %. Lisää johtopäätöksiä kulutuksen ja tulojen välisestä riippuvuudesta voidaan tehdä ekonometrisilla menetelmillä.
Merkitään taulukossa T3.1 esitetyt tiedot kulutuksesta C ja vastaavista tuloista Y koordinaatistoon kuvion K3.2 tapaan. Koska pistejoukko näyttää jossain määrin kaartuvan oikealle alaspäin, siihen sovitetaan tilastotieteen peruskursseilla lähemmin esiteltävän pienimmän neliösumman (PNS) periaatteen mukaisesti koulumatematiikasta tuttu paraabeli.
C = a + b Y + c Y2
Tämä tapahtuu kätevästi millä hyvänsä standarditietokoneohjelmalla, kunhan ensin tulohavannoista muodostetaan toiseksi selittäväksi muuttujaksi tulon neliö Y2 (232 = 529, 362 = 1296, jne.)
Tämän operaation tarkoituksena on löytää paraabelin parametreille a, b ja c tässä annettujen kulutusta ja tuloa koskevien tietojen perusteella numeroarvot. Niiden perusteella määräytyy paraabelin sijainti pistejoukossa eli se lainalaisuus, joka kulutus- ja tulohavaintojen välillä vallitsee. Saadaan alaspäin aukeava (miinus-merkkinen neliötermin kerroin) paraabeli
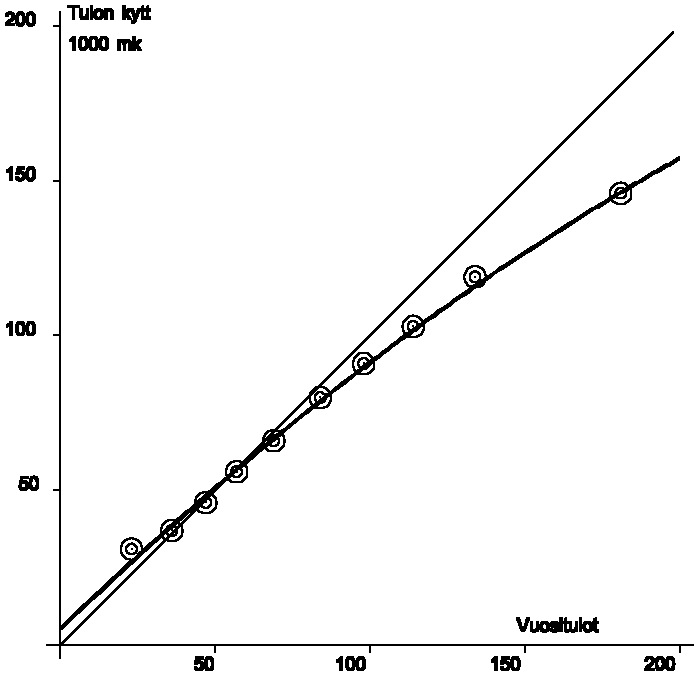
C = 5.32 + .967 Y - .0010 Y2
Tässä emme puutu tämän kulutusfunktioksi nimetyn mallin tilastollisiin omi-naisuuksiin. Sen sijaan voimme käyttää tätä mallia kahdenlaisen informaa-tion tuottamiseen:
1. Kulutuksen suuruus eri tulotasoilla saadaan helposti selville sijoittamalla kulutusfunktioon Y:n paikalle haluttuja tulotason arvoja. Esim. Y = 70 (tuhatta markkaa) C = 5.32 + .967*70 - .0010*702 = 5.32 + 67.69 - 4.9 = 68.11 Taulukkoon T3.2 on tällä tavoin laskettu kulutuksen todennäköisiä suuruuksia eräillä tulotasoilla.
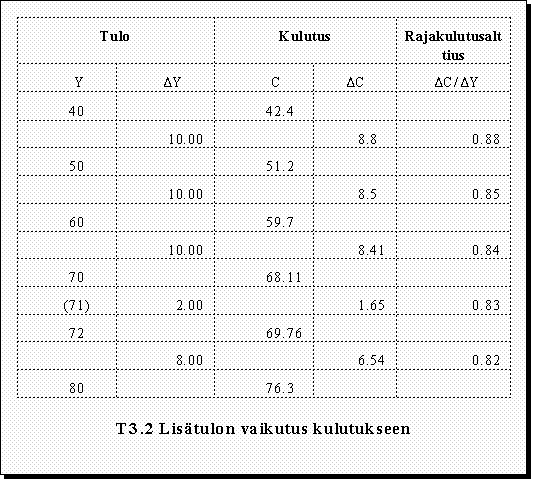
2. Kulutuksen muutos. Tulojen muutoksesta aiheutuva kulutuksen muutos tulomuutoksen yksikköä kohti eli rajakulutusalttius tai rajakulutusosuus voidaan laskea kulutusfunktion avulla. Rajakulutusalttiuden selvittämiseksi laskemme kulutukfunktiosta kulutuksen arvon, kun tulot Y = 72
C = 5.32 + .967*72 - .0010*722
= 5.32 + 69.62 - 5.18 = 69.76
Vertaamme nyt saatua kulutuksen arvoa edellä laskettuun. Jakamalla kulutuksen muutos (69.76-68.11=) 1.65 tapahtuneella tulon muutoksella (72-70=) 2 saamme rajakulutusalttiuden.
MPC = 1.65/2 = .83
Rajakulutusalttius ilmaisee siis, montako (tuhatta) markkaa tällä tulotasolla käytetään kulutukseen, jos tulo lisääntyy (tuhannella) markalla. Tässä 1000 markan tulonlisäys aiheuttaa 830 markan kulutuksen lisäyksen. Tai jos tulo lisääntyy 1 markalla, siitä aiheutuu 83 pennin kulutuksen lisäys.
Havaitaan, että rajakulutusalttius alenee korkeammalle tulotasolle siirryttäessä. Siirryttäessä tulotasolta Y = 40 tulotasolle Y = 50 jokainen tuhannen markan tulonlisäys aiheuttaa keskimäärin (.88*1000=) 880 markan suuruisen kulutuksen lisäyksen. Mitä tehdään lopulle 120 markalle? Ne säästetään tai niillä pienennetään velkoja. Vastaavasti siirryttäessä 72 tuhannen tulotasolta 80 tuhannen tulotasolle kulutus nielaisee tulojen lisätuhannesta noin 820 mk, loput 180 mk jäävät säästöön. Koska tulojen käytössä on vain kaksi vaihtoehtoa: kulutus ja säästäminen, määräytyy säästäminen automaattisesti sen jälkeen, kun kulutus on ensin määräytynyt. Säästäminen S on yksinkertaisesti tulojen ja kulutuksen erotus eli
S = Y - C
Tämän mukaisesti kulutusfunktiota voidaan johtaa säästämisfunktio. Tässä esimerkkitapauksessa saadaan
S = Y - (5.32+.967 Y - .0010 Y2)
= - 5.32 + .033 Y + .0010 Y2
Myös muut seikat kuin tulot vaikuttavat kuluttajan käyttäytymiseen. Sellaiset tekijät kuin perheen koko ja sosioekonominen asema ovat kuluttajan elinolosuhteiden osalta tärkeitä kulutukseen vaikuttavia tekijöitä. Markkinailmiöistä taas hyödykkeiden väliset hintasuhteet ovat tärkeitä.
Esimerkiksi tässä tarkastelussa vuoden 1985 kulutustutkimuksessa on tulo-desiileittäin (näyte jaettu tulojen suuruuden mukaan kymmenen luokkaan) tietoja myös perheen koosta, joten sen vaikutusta voidaan tarkastella erikseen. Perheen koon H ottaminen kulutusta C selittäväksi muuttujaksi tulon Y neliötermin asemesta antaa kulutusfunktion
C = 10.0 + .67 Y + 4.9 H
Jos tällä kulutusfunktiolla suoritetaan laskelmia sijoittaen Y:n ja H:n arvoja, havaitaan, että
Edellä on käsitelty kuluttajan käyttäytymistä tavallaan ilman vaihtoehtoja. Kysymyksenasetteluna on ollut: Kuluttaako vai ei? tai Kuinka paljon kuluttaa? Vähintään yhtä mielekäs kysymyksenasettelu on: Minkä vaihtoehdon kuluttaja valitsee? Tai Milloin kuluttaja tuntee käyttäneensä ostovoimansa parhaalla mahdollisella tavalla? Eräs tapa tarkastella kuluttajatalouden valintaongelmaa on vertailla kahden hyödykkeen välistä valintatilannetta budjettisuoran avulla.
Oletetaan, että kuluttajalla on käytettavissään ruuan ja vaatteiden hankintaan 500 mk kuukaudessa. Lisäksi oletetaan, että ruoka ja vaatteet ovat 'homogenisoitavissa' ravintoyksiköiksi, esim. kilokaloreiksi ja sukkapareiksi, joiden hinnat ovat 4 mk/kcal ja 5 mk/pari. Jos kuluttaja käyttäisi kaikki rahansa ruokaan, hän saisi 500 markalla 125 kilokaloria ruokaa (500/4=125). Jos taas hän käyttäisi kaikki rahansa vaatteisiin, hän voisi ostaa niitä 100 sukkaparin edestä (500/5=100). Ainakaan jälkimmäinen vaihtoehto ei voi tulla kysymykseen, sillä ilman ruokaa ei kukaan tule toimeen.
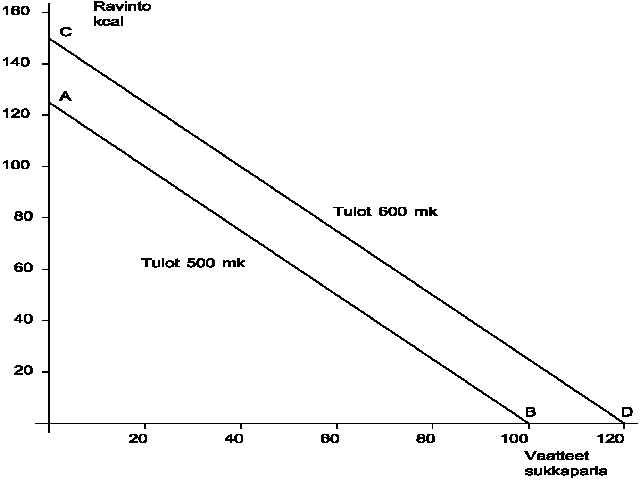
Todellisuudessa kuluttaja jakaa tulonsa osaksi molempien hyödykeryhmien kesken: 500 markkaa on mahdollista jakaa näiden kahden hyödykkeen kesken esim. siten, että ostetaan 100 kcal ruokaa ja 20 sukkaparin edestä vaatteita (100*4 + 20*5 = 500) tai 80 kcal ruokaa ja 36 sukkaparin edestä vaatteita (80*4 + 36*5 = 500). Saattaisipa joku koreilunhaluinen tyytyä 60 kcal ruoka-annokseen ja ostaa peräti 52 sukkaparin edestä hepeniä. Teoreettisesti kaikki suoran AB pisteet kuviossa K3.3 ovat mahdollisia yhdistelmiä.
Edellisestä tarkastelusta nähdään vielä, että kuluttajan luopuessa 20 kilokalorista ruokaa hän saa 16 sukkaparin edestä vaatteita eli yhdellä kilokalorilla 0.8 paria sukkia tai paremminkin toisinpäin yhdellä sukkaparilla 1.25 kilokalorin verran ravintoa. Edellytyksenä on siis koko ajan, että näihin hyödykkeisiin on käytettävissä 500 mk ja hinnat ovat 4 mk/kcal ja 5 mk/sukkapari.
1. Tulovaikutus. Mitä tapahtuu budjettisuoralle,jos näihin menoihin käytettävät tulot kasvavat 600 markkaan kuukaudessa ilman, että hinnat muuttuvat? Jakamalla 600 mk vuoron perään hinnoilla 4 ja 5 löydetään uuden budjettisuoran ja akselien leikkauspisteet C=150 ja D=120. Nähdään, että budjettisuora siirtyy suuntaansa säilyttäen kauemmaksi nollapisteestä. Kuluttaja voi nyt ostaa niin halutessaan molempia hyödykkeitä enemmän kuin tähän asti. Jos taas käytettävissä oleva tulo pienenee, siirtyy budjettisuora vastaavasti suuntansa säilyttäen lähemmäksi nollapistettä siten rajoittaen molempien hyödykkeiden kulutusmahdollisuuksia.
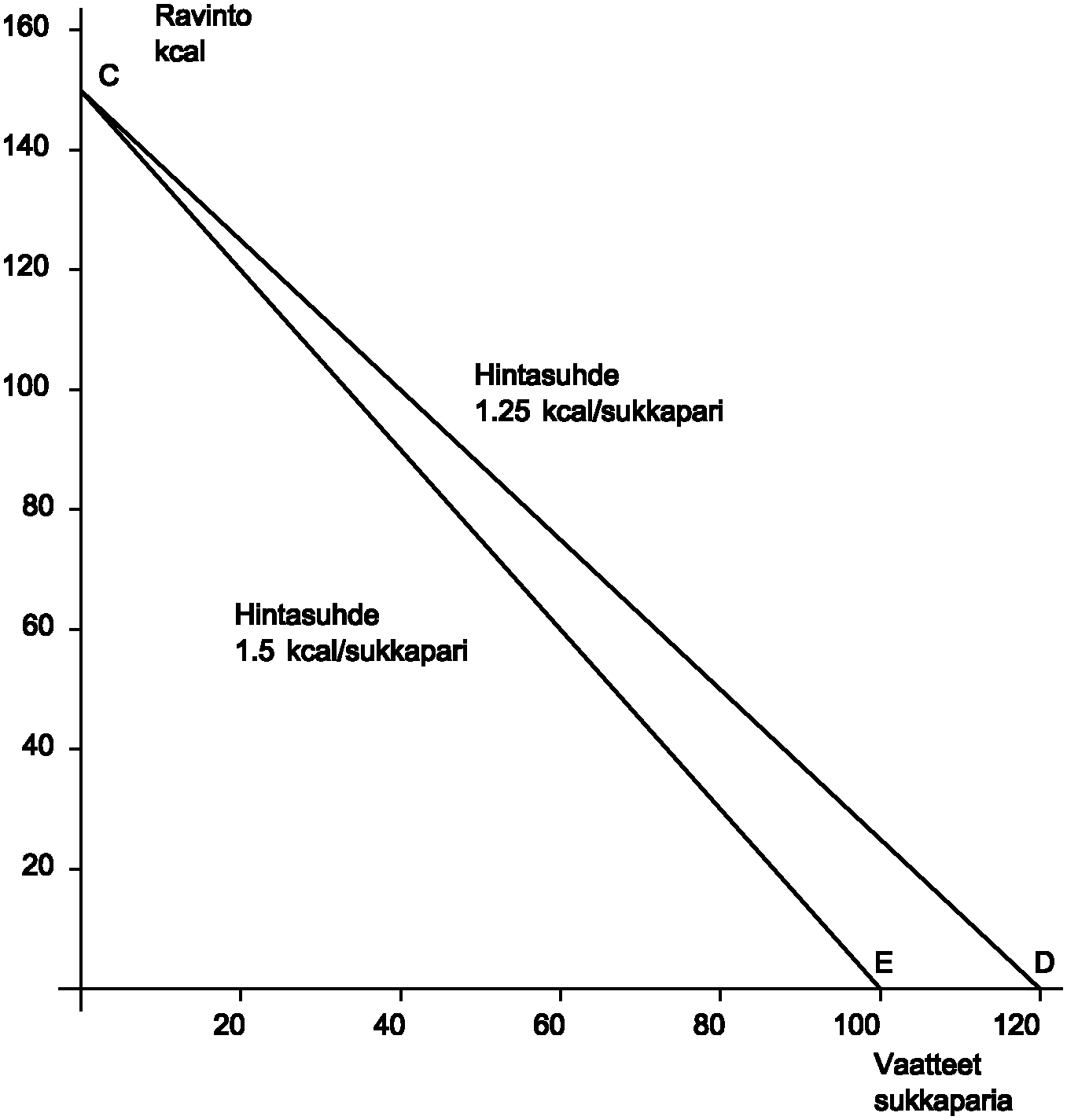
2. Hintavaikutus. Entä mitä tapahtuu, jos jompi kumpi hinnoista muuttuu? Oletetaan esim., että sukkaparin hinta nousee 6 markkaan. Jos käytettävissä on 600 markkaa, saisi kuluttaja edelleen 150 kcal ruokaa mutta vain 100 sukkaparin edestä vaatteita, mikäli hän käyttäisi kaikki rahansa jompaan kumpaan. Hintasuhde on nyt 1.5 kcal ruokaa/sukkapari. Halutessaan molempia hän saa esim 120 kcal ruokaa ja 20 sukkaparin edestä vaatteita (120x4 + 20x6 = 600) tai minkä hyvänsä suoran CE kuviossa K3.4 antamista yhdistelmistä ruokaa ja vaatteita. Samanlainen tarkastelu voidaan tietysti suorittaa ruuan hinnan noustessa ja vaatteiden hinnan pysyessä ennallaan. Tulojen säilyessä ennallaan ja toisen hinnan noustessa joudutaan todennäköisesti molempien hyödykkeiden kulutusta vähentämään, enemmän tingitään sen hyödykkeen kulutuksesta, jonka hinta nousi ja vähemmän sen, jonka hinta pysyi ennallaan. Sitä, että kuluttajan käyttämien hyödykemäärien osuudet kokonaiskulutuksesta muuttuvat, sanotaan hintasuhteen muutoksen substituutio- eli korvausvaikutukseksi.
Mutta mitä tapahtuu, jos molemmat hinnat hinnat muuttuvat? Jos molemmat hinnat nousevat samassa suhteessa, esim. 20% eli ruuan hinta nousee 4 markasta 4.80 markkaan kilokalorilta ja vaatteiden 5 markasta 6 markkaan sukkaparilta hintasuhteen siis säilyessä ennallaan eli parilla sukkia 1.25 kilokaloria ravintoa, on se sama, kuin jos käytettävissä oleva tulo alenisi 20 prosenttia eli 600 markasta 500 markkaan. Hintojen muutos hintasuhteen säilyessä ennallaan kääntyykin siis itse asiassa tulovaikutukseksi. Jos taas hinnat muuttuvat siten, että samalla hintasuhde muuttuu, on osa kokonaismuutoksesta hintavaikutusta ja osa tulovaikutusta.
Vieläkin syvemmälle kuin tulojen ja hintojen vaikutuksiin on porauduttava mikäli halutaan perin pohjin selvittää kuluttajan käyttäytymiseen vaikuttavat tekijät. Pohjimmiltaan kuluttajan käyttäytyminen on psykologinen ilmiö, jolle taloudelliset seikat vain asettavat puitteet.
Tästä on kysymys, kun tarkastellaan rajahyötyteoriaa, erästä vanhimmista kuluttajan käyttäytymistä koskevista teorioista. Tässä teoriassa on keskeistä selvän eron tekeminen rajahyödyn ja kokonaishyödyn välillä. Tämän eron havaitsemista on sanottu erääksi taloustieteen hienoimmista oivalluksista. Kuluttajan kokemaa psyykkistä tyydytystä jonkin hyödykkeen käyttämisestä nimitetään kuluttajan saamaksi hyödyksi. Ero jonkin hyödykkeen käytön antaman kokonaishyödyn ja siitä saatavan rajahyödyn välillä ymmärretään, jos tarkastellaan kuluttajien antamia vastauksia seuraavan kahteen kysymykseen:
Kysymyksessä 1 verrataan vedestä saatavaa kokonaishyötyä bingon pelaamisesta saatavaan kokonaishyötyyn. Tosi paikan tullen tuskin kukaan epäröisi, vaan valitsisi veden. Onneksi tällainen valintatilanne on epätodellinen eikä muidenkaan hyödykkeiden osalta tule kovin usein kysymykseen.
Kysymyksen 2 mukaisessa valintatilanteessa olemme jatkuvasti. Kysymys on siitä, miten arvostamme kylvyn suuruista lisää vedenkulutuksessamme verrattuna yhteen pelikierrokseen bingossa, vastakkain ovat kahden hyödykkeen rajahyödyt. Emme voi ilman muuta olla niinkään varmoja, miten eri henkilöt vastaisivat tähän kysymykseen. Kukin valitsee makunsa mukaan. Jos kuluttajan tulot nousevat hiukan, on hänen ratkaistava, mihin hyödykkeisiin hän lisätulonsa käyttää. Vastaavasti tulojen pienentyessä (tai hintojen noustessa) on ratkaistava, mistä hyödykkeistä on luovuttava. Tässä rajahyöty ratkaisee.
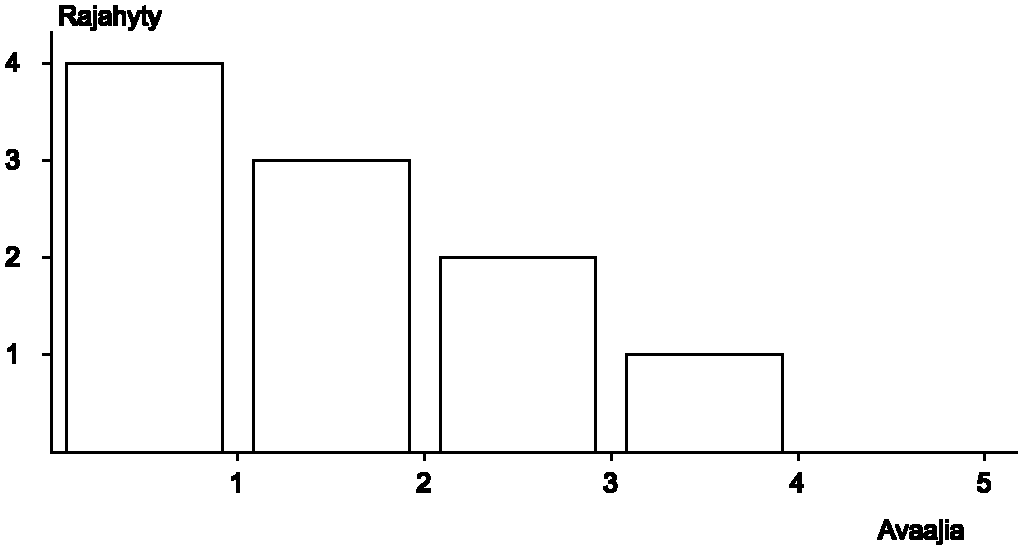
Rajahyötyteorian perushypoteesi on:
Kuluttaessaan lisää jotakin hyödykettä kuluttajan saama kokonaishyöty voi tosin kasvaa, mutta jokaisen lisää kulutetun hyödykkeen antama rajahyöty alenee.
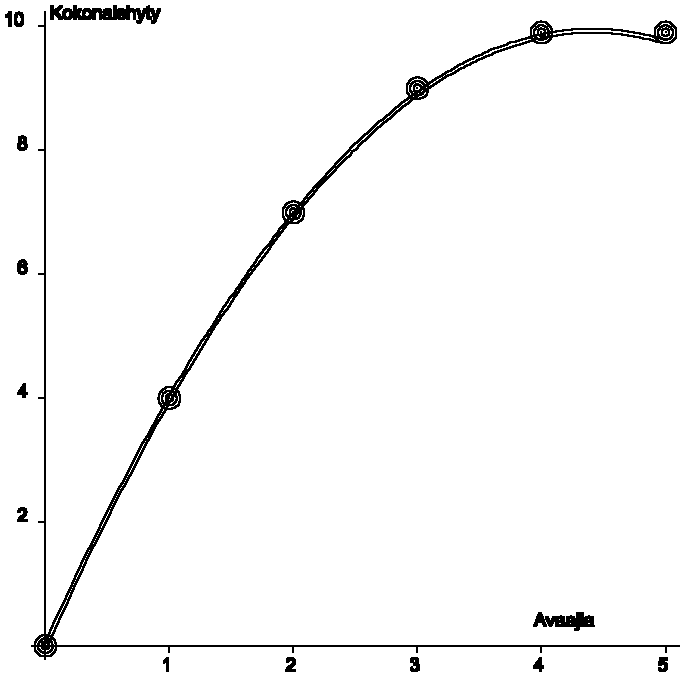
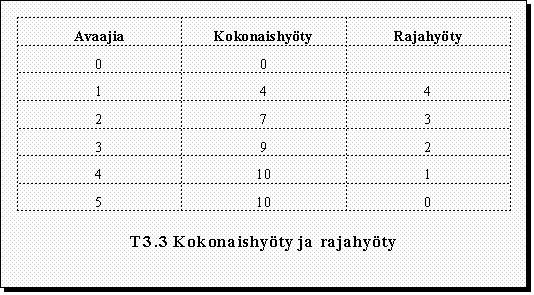
Tätä perustavaa laatua olevaa alenevan rajahyödyn teoriaa voidaan valaista esimerkillä kruunukorkin avaajasta kesämökillä. Ellei kesämökillä satu olemaan lainkaan kruunukorkin avaajaa, on pakko valikoida juomansa tai muuten pöydän reunat ovat vaarassa. Hyöty olemattomasta avaajasta on tietenkin nolla ('hyötypistettä'). Yhdestä avaajasta on suuri hyöty, varsinkin jos sen kiinnittää narulla seinään, ettei se pääse hukkaantumaan. Toinen avaaja tuottaa myös lisähyötyä. Sen voi esim. viedä saunalle. Kolmannestakin voi olla hyötyä, mutta tuskin niin suurta lisähyötyä (=rajahyöty) kuin ensimmäisestä ja toisesta. Tässä esimerkissä on ajateltu vielä neljännenkin avaaja tuottavan pisteen verran lisähyötyä. Mutta viides tuskin antaa mitään lisämielihyvää. Liioista avaajista saattaa todellisuudessa olla jopa haitta eli miinus-merkkistä hyötyä.
1. Kulutuksen suuruus määräytyy suurimmaksi osaksi kuluttajan tulojen mukaan, mutta valinta vaihtoehtojen välillä tehdään hyötyä ja hintaa vertaamalla.
2. Tulojen kasvaessa kulutuksen osuus tuloista alenee ja säästämisen osuus kasvaa. Alimmissa tuloluokissa perheen omat tulot eivät riitä kulutukseen, ja säästämisen sijasta joudutaan velkaantumaan. Tietyllä tulotasolla tulot juuri riittävät kulutukseen. Tämän tulotason yläpuolella voidaan säästää.
3. Tilastotietojen perusteella voidaan laatia kulutusfunktio, joka kuvaa kulutuksen ja tulojen välistä riippuvuutta. Kulutusfunktiosta voidaan laskea (1) todennäköisiä kulutuksen arvoja halutulla tulotasolla ja (2) rajakulutusalttius eli tieto siitä, paljonko kulutus muuttuu, kun tulot muuttuvat yhdellä yksiköllä.
4. Säästäminen on se, mitä jää tuloista kulutuksen jälkeen jäljelle.
5. Tulojen ohella perheen koko on tärkeä kulutuksen suuruuteen vaikuttava tekijä.
1. Budjettisuoran avulla voidaan tarkastella erikseen tulon muutoksen ja hintojen muutoksen vaikutusta kuluttajatalouden valinta-ongelmaan.
2. Kuluttajan käyttäytymisen perimmäinen selitys on rajahyötyteo-riassa, jossa tarkoin erotetaan toisistaan kuluttajan hyödykkeen käytöstä saama kokonaishyöty ja rajahyöty. Rajahyöty on lisähyöty hyödykkeen lisäkäytöstä. Hyödykkeen käytön lisääntyessä kokonaishyöty kasvaa rajahyöty alenee.
Alkuun o Yksityiskohtainen sisällysluettelo o AJK kansantalouden kurssit o AJK kotisivu
Asko Korpela, kansantaloustieteen lehtori, Helsingin kauppakorkeakoulu
Asko Korpela 970818 (960929) o Asko.Korpela@kolumbus.fi
[ccc]