Asko Korpela: Kansantalouden peruskurssi:
Osa 3 KANSANTALOUDEN TASAPAINO
(Asko.Korpela@kolumbus.fi) o Sisällysluettelo
o AJK kurssit o AJK
kotisivu
8.1 Kulutusfunktion teoriaa
o Kulutusfunktio poikkileikkausaineistosta
o Kulutusfunktio aikasarjasta
8.2 Kulutus ja tasapaino
o Ekonometrinen kokonaismalli
Yhteenveto: Kulutus ja tasapaino
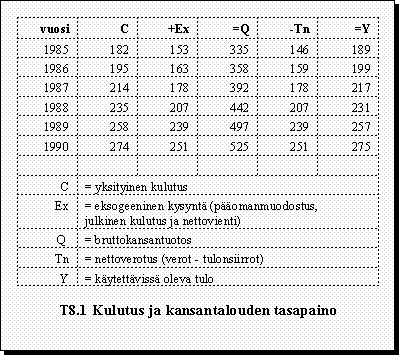
Taulukko: T8.1 Kulutus
ja kansantalouden tasapaino
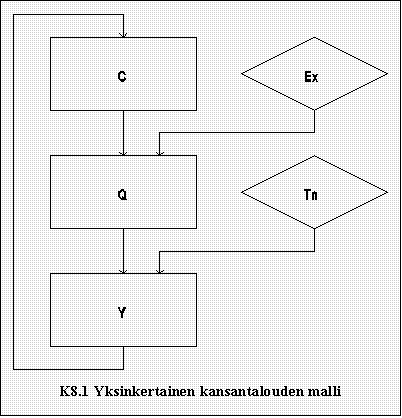
Kuvio: K8.1 Yksinkertainen
kansantalouden malli
Tähän mennessä olemme tarkastelleet kulutuksen peruspäätäntäyksikön, perheen käyttäytymistä ja perheen kulutuksen riippuvuutta perheen tuloista. Suomen kansantalouden kulutussektorin muodostaa yli kaksi miljoonaa perhettä. On selvää, että kansantalouden kokonaiskulutuksen määrä riippuu kansantalouden kokonaistulosta samaan tapaan kuin perheen kulutus perheen käytettävissä olevasta tulosta.
Siirryttäessä näin mikrotasolta eli yhden päätöksentekijän - tässä perhe - tasolta makrotasolle eli koko kansantalouden tasolle joudutaan myös tarkastelun pohjana olevat empiiriset havainnot keräämään toisella tavalla. Edellä perheen kulutusfunktiota tarkasteltaessa havainnot olivat poikkileikkausaineistosta. Poikkileikkaustiedot kerätään lyhyenä ajanjaksona tai määrätyllä hetkellä joukolta taloudellisia päätäntäyksiköitä. Taloudellisten tapahtumien virrasta otetaan poikkileikkauskuvio määrätyllä hetkellä ikään kuin makkarasta siivu. Perusolettamuksena poikkileikkaustutkimuksessa on, että perhe A käyttäisi esim. ravintoon yhtä suuren osan tuloistaan kuin perhe B, jos molempien perheiden tulot olisivat yhtä suuret. Tutkittaessa poikkileikkusaineistosta muodostettua kulutusfunktiota on siis perusongel-mana:
Miten perheen kulutus riippuu sen tuloista (ja suuruudesta yms.)?
Muiden tekijöiden (perheen koko, ikärakenne, asuinpaikka) vaikutuksia pyritään vähentämään
1. muodostamalla näiden suhteen mahdollisimman homogeenisia luokkia, joista kustakin estimoidaan erillinen kulutusfunktio tai
2. ottamalla näitä tekijöitä lisäselittäjiksi kuten edellä on menetelty perheen koon suhteen.
Poikkileikkaustutkimuksen avulla koottua tilastoaineistoa käytetään erityi-sesti kuluttajan hintaindeksin pohjana. Hintaindeksiä varten kerättävät tiedot painotetaan ryhmäindeksien ja yleisindeksin muodostamista varten asian-omaisen hyödykkeen osuudella kuluttajan kokonaismenoista.
Poikkileikkaustiedot koskevat eri kulutusyksiköitä määrättynä ajankohtana. Niissä vertaillaan eri perheitä eri tulotasolla. Aikasarjatietojen kerääminen on toinen tapa saada tietoja kuluttajan käyttäytymisestä. Silloin tarkastellaan periaatteessa samaa päätöksentekijää tai päätöksentekijäjoukkoa eri ajankohtina ja eri tulotasoilla. Kokonaistaloudellisessa tai sektorikohtaisessa tarkastelussa aikasarjat ovat ilman muuta yleisempi ja käytetympi tiedonhankintamenetelmä. Poikkileikkaustiedoista saadaan käsitys siitä, kuinka kulutusmenot muuttuvat tulotason mukaan määrätyllä hetkellä, kun taas aikasarja-aineistosta saadaan valaisua kysymykseen: kuinka kulutus muuttuu, jos kaikkien kotitalouksien tulot muuttuvat.
1. Pitkän tähtäyksen kulutusfunktio. Käyttämällä selittävän tulomuuttujan viivästettyjä havaintoja hyväksi voidaan päästä irti useista lyhyellä tähtäyksellä kulutukseen vaikuttavista tekijöistä. Havaitaan, että keskimääräinen kulutusosuus (APC Average Propensity to Consume) ja rajakulutusosuus (MPC Marginal P. to C.) ovat alle yhden, mutta APC ei alene tulojen kasvaessa. Tällöin APC ja MPC ovat hyvin lähellä toisiaan, mikä graafisessa esityksessä näkyy siinä, että kulutusfunktio leikka pystyakselin lähellä nollaa.
2. Lyhyen tähtäyksen kulutusfunktio. Selittämällä kulutusta pelkästään saman ajankohdan tulohavainnoilla havaitaan, että rajakulutusosuus on pienempi kuin yksi, mutta kuitenkin korkeampi kuin poikkileikkaus-tutkimuksessa saatu. Keskimääräinen kulutusosuus alenee tulojen noustessa. Erotukseksi pitkän tähtäyksen kulutusfunktiosta rajakulutusosuus on lyhyen tähtäyksen kulutusfunktiossa pienempi kuin keskimääräinen kulutusosuus, joten kuluttajat käyttävät siis suhteellisesti sitä pienemmän osan lisätulois-taan kulutukseen, mitä korkeammalla tulotasolla he ovat.
3. Hyvin lyhyen tähtäyksen kulutusfunktio. Jos käytetään neljännesvuosi-havaintoja, todetaan, että kulutuksen ja tulojen välinen riippuvuus on huomattavasti heikompi kuin edellisissä tapauksissa. Tästä voidaan tehdä se johtopäätös, että lyhyen tähtäyksen muutokset kulutuksessa eivät johdu pääasiassa lyhyen tähtäyksen muutoksista tulotasossa.
Lyhyen tähtäyksen kulutusfunktiota tutkittaessa on päädytty kulutuksen jakamiseen vähintään kahteen komponenttiin, nimittäin kestokulutushyödykkeisiin ja muihin kulutushyödykkeisiin.
Tällöin havaitaan, että
1. lyhyen tähtäyksen muutoksista suurin osa tapahtuu juuri kestokulutushyödykkeiden kohdalla.
2. kestokulutushyödykkeiden ostaminen reagoi sellaisiin seikkoihin kuin korkotasoon, vähittäismaksuehtoihin ja tulo-odotuksiin. Näihin eivät muut kulutushyödykkeet reagoi läheskään samassa määrin.
3. mainitut seikat saattavat olla jopa tärkeämpiä kuin tulo selitettäessä hyvin lyhyen tähtäyksen kulutuskäyttäytymistä.
Jos kulutusfunktio muodostetaan aikasarjasta, havaitaan myös, ettei siirtyminen korkeammalle tulotasolle pienennä rajakulutusosuutta eikä siis käyräviivainen funktiomuoto ole mallia laskettaessa lainkaan tarpeen.
Kansantalouden tilinpidon tiedoista voidaan tilastotieteen oppikirjoissa tarkemmin selostetulla pienimmän neliösumman (PNS) menetelmällä laskea kulutuksen ja tulojen välinen numeerinen riippuvuus eli kulutusfunktio. Kulutusfunktion avulla voidaan vastata kysymyksiin: Kuinka suuri on kulutus, jos tulojen suuruus tiedetään? Paljonko kulutus muuttuu, jos tulot muuttuvat?
Vuosien 1962-90 havaintoaineistosta tämä empiiriseen tietoon perustuva kansantalouden kulutusfunktio on yksinkertaisimmassa muodossaan
C = .4 + .58 C1 + .46 Y
C = yksityinen kulutus
C1 = edellisen vuoden kulutus
Y = käytettävissä olevat tulot

Tarkastellaan vuoden 1990 kulutuksen määräytymistä. Jos nyt edellisen vuoden eli vuoden 1989 kulutus oli 258 mrd mk ja vuoden 1990 tulot ovat 275 mrd mk, saadaan kulutusfunktiota käyttäen vuoden 1990 kulutuksen arvioksi 276 mrd mk.
276 = .4 + .58 (258) + .46 (275)
Koska tarkastellaan vuotta 1990, on kulutuksen todellinen arvo jo tiedossa. Se on 274 mrd mk. Mallin virhe oli siis 2 mrd mk Se tuntuu merkityksettömän pieneltä. Luotettavan kuvan tämän kansantalouden kulutusfunktion selityskyvystä saisimme laskemalla sen avulla yksityisen kulutuksen arvoja useille vuosille ja vertaamalla niitä vastaaviin havaintoihin.
Tässä vaiheessa olemme siis selvittäneet yhden kokonaiskysynnän komponentin, yksityisen kulutuksen riippuvuuden tuloista. Seuraavassa luvussa selvitetään pääomanmuodostukseen vaikuttavia tekijöitä ja niiden vaikutuksen suutuutta. Mutta jo nyt voimme laatia Suomen kansantaloutta kuvaavan ekonometrisen mallin.
C = .4 + .58 C1 + .46 Y
Q = C + Ex
Y = Q - Tn
Tässä mallissa on kolme yhtälöä ja viisi muuttujaa. Kuudes muuttuja C1 tarkoittaa viivästettyä kulutusta. Siis esim. vuonna 1990 käytetään vuoden 1989 kulutuksen arvoa C1 = 258.
Tällä tavalla laaditun mallin hyöty on siinä, että jos tiedetään tai voidaan erikseen arvioida muuttujien Ex ja Tn arvot, voidaan loput kolme: C, Q ja Y laskea ratkaisemalla tämä kolmen yhtälön ryhmä.
Tässä mallissa määräytyy siis paitsi kulutus tulojen perusteella, myös toisensuuntainen vaikutus eli se, miten tulot riippuvat kulutuskysynnästä. Tämä kansantalouden malli on esitetty lohkokaaviona kuviossa K8.1.
Lohkokaaviosta nähdään selvästi kuinka eksogeeniset muuttujat Ex ja Tn vaikuttavat malliin endogeenisiin muuttujiin C, Q ja Y. Endogeeniset muuttujat vaikuttavat joko välittömästi tai välillisesti toisiinsa, mutta eivät eksogeenisiin. Kansantalous on juuri tällainen keskinäisten riippuvuuksien järjestelmä, jossa 'kaikki vaikuttaa kaikkeen' - tai ainakin hyvin monet seikat ovat keskinäisessä riippuvuussuhteessa.
Jos nyt tiedetään, että kulutus vuonna 1990 on 274 mrd mk ja voidaan olettaa, että eksogeeninen kysyntä ja nettoverotus ovat vuonna 1991 Ex = 240 mrd mk ja Tn = 255 mrd mk, voidaan tämä yksinkertainen malli esim. taskulaskinta käyttäen ratkaista. Silloin saadaan kulutuksen, bruttokansan-tuotoksen ja käytettävissä olevan tulon ennusteet vuodelle 1991. Tarkista, että ne ovat näillä olettamuksilla:
C = 282 Q = 522 Y = 267 (mrd mk)
Tämä malli on pieni ja voidaan suhteellisen helposti ratkaista. Tietokoneella voidaan yhtä helposti rakentaa ja käsitellä paljon laajempia malleja. Niiden selityskykyä voidaan tutkia, ja niillä voidaan laatia suhteellisen luotettavia ja yksityskohtaisia ennusteita ja talouspoliittisia vaihtoehtolaskelmia.
1. Kulutusfunktio poikkileikkausaineistosta laaditaan keräämällä saman ajankohdan tietoja joukolta taloudellisia päätäntäyksiköitä. Poikkileikkaustutkimuksessa verrataan eri päätöksentekoyksiköiden suhtautumista määrätyn taloudellisen muuttuja arvoihin.
2. Aikasarjatutkimuksessa on tutkimuksen kohteena saman päätäntäyksikön käyttäytyminen eri ajanjaksojen kuluessa tai eri ajankohtina.
3. Pitkän tähtäyksen kulutusfunktiossa vakiotermi on pieni ja raja-kulutusalttius lähellä keskimääräistä kulutusalttiutta. Lyhyen tähtäyksen kulutusfunktiossa rajakulutusalttius on selvästi pienempi kuin keskimääräinen kulutusalttius. Hyvin lyhyen tähtäyksen kulutusfunktiossa muut tekijät kuin tulo ovat tärkeitä.
Alkuun o Sisällysluettelo o AJK kurssit o AJK kotisivu
Asko Korpela 970818 (960929) o Asko.Korpela@kolumbus.fi
[ccc]