07 Pääomanmuodostus heilahtelee
1 Pääomanmuodostus
ja kiihdytinperiaate
o Paperin tuotanto
o Taulukko: kiihdytin
o Kiihdytinteorian matematisointi
2 Odotukset ja pääomakanta
(joustava kiihdytin)
o Varannon sopeutus
o Odotukset
3 Pääomanmuodostus
ja rahoitusmahdollisuudet
o Markkinakorko
o Reaalikorko
o Hallinnollinen korko
4 Pääomanmuodostus
hyödykeryhmittäin
Harjoitustehtävän idea
Tietokoneohjelmat: Muuttujien tarkastelu TreGraf
o Regressiolaskelmat SuoKok
Käsitteitä: Paperin tuotanto o
Taulukko: Kiihdytin o Reaalikorko
o Lähdeviitteitä
Kuviot: paperikone o poistot
o rakennusprojekti o korkoneuvottelu
o tieprojekti
H07 Harjoitustehtävä o Makroteoria ja Suomen kansantalous o Kansantalouden kurssit o AJK kotisivu
Pääomanmuodostusta koskevaa päätöksentekoa on vaikea pätevästi selittää tai ennustaa, sillä pääomahyödykkeiden hankintoja voidaan helposti siirtää ajassa eteen- tai taaksepäin. Pieni tuotannon vaihtelu voi aiheuttaa samansuuruisen muutoksen pääomakannassa, mutta monin-kertaisen suhteellisen muutoksen pääomahyödykkeiden hankinnoissa.
Kulutuskysynnän riippuvuuksien ymmärtämisessä oleellinen asia oli sopivan tulokäsitteen määrittely. Lopulta päädyttiin periaatteessa kaikenkattavaan 'aikojen alusta ikuisuuteen' elinkaarihypoteesiin. Se antoi myös tilastollisesti parhaan selityskyvyn. Mutta jo vaatimattomimmallakin tulohypoteesilla päästään kohtuulliseen selityskykyyn ja, kuten myöhemmin nähdään, myös varsin hyvään ennustetarkkuuteen. Toisin on asia pääomanmuodostuksssa. Ei ole olemassa mitään hyvää teoriaa, jonka avulla voitaisiin selittää yrittäjän investointipäätökiä tai pääomanmuodostusta kansantalouden kokonaisnäkökulmasta läheskään yhtä tarkasti kuin voidaan ymmärtää ja ennustaa kulutusta. Ei edes usean teorian yhdistelmillä päästä ennustevirheellä mitaten kuin korkeintaan puoleen siitä selityskyvystä, johon kulutuksessa päästään.
Siitä huolimatta haaste on otettava vastaan, ja pääomanmuodostusta yritetään tässä mekanisoida malliksi sekä mikrotasolla että makrotasolla. Onneksi pääomanmuodostus on bruttokansantuotoksen komponenttina korkeintaan puolet yksityisen kulutuksen suuruudesta, joten malli ei kärsi täydellistä haaksirikkoa tämän komponentin virheellisyyden takia. Syy pääomanmuodostuskomponentin ongel-mallisuuteen on sen luonteessa.
Pääomanmuodostusta voidaan samalla tavoin kuin kestokulutushyödykkeiden hankintoja siirtää ajassa eteenpäin tai taaksepäin kovin helposti. Tämän takia pääomanmuodostus voi jonakin vuonna kasvaa rajusti ja jonakin toisena taas pysyä entisen suuruisena tai jopa supistua, kun olemassa olevasta pääomakannasta poistuu loppuun käytettyjä pääomahyödykkeitä: koneita, kalustoa, rakennuksia.
Ja kun tällaisen ruuhkautuneen pääomahyödykkeiden hankintarysäyksen aikana hankitut pääomahyödykkeet sitten kuluvat loppuun ja ne poistetaan käytöstä, sekin tapahtuu suunnilleen samanaikaisesti tietyn luonnollisen käyttöiän jälkeen. Näin syntyy uusi ruuhkautuma ja ruuhkautuman jälkeen suvantovaihe, koska niin suuri osa pääomakannasta on juri uusittu. Näin syntyy itse asiassa suhdannevaihtelu. Selvin esimerkki tästä ovat sotien jälkeiset rakennusboomit. Sota tuhoaa. Sodan jälkeen rakennetaan nopeasti uudet. Uusien rakennusten käyttöiän kuluttua tarvitaan taas uudet korvaamaan käytöstä poistetut.
|
K7.1 Pääomanmuodostus Suomen kansantaloudessa,
mrd 90 mk |
IFAF Kiinteän pääoman bruttomuodostus mrd 90 mk 96026 ExpTrend: 71-95 0.2%, 86-95 -5.9% 61 57.4 57.8 56.0 59.3 65.7 68.3 67.4 63.9 72.1 81.0 71 84.1 89.3 97.2 100.5 106.5 96.8 93.5 87.0 89.6 99.0 81 101.1 105.7 109.9 107.6 110.1 109.7 115.1 126.4 145.1 139.1 91 111.0 92.2 74.5 74.6 80.4 |
| Kuviosta nähdään investointien kehitys vuosina 1961-95. Vuoden 1995 trendiarvo sattuu aivan havainnon kohdalle, joten trendiennuste ja trendiarvo vuodelle 1995 ovat samat. Vaihtelu trendin molemmin puolin on investoinneissa suurempaa kuin kulutuksessa ja investoinnit ovat useaan kertaan supistuneet edellisestä vuodesta, vuosina 76-78 kolmena vuonna ja 90-93 jopa neljänä vuonna peräkkäin. |
| Kokeile tietokoneohjelmaa! | |
| TREGRAZZ.exe | Aikasarjatietokannan grafiikka ja trendit |
| Ohjelmapaketin tallennus kansioon c:\tmp
Kaksoisnäpäytä TREGRAZZ Kaksoisnäpäytä SetupTRE.bat TREGRAF.EXE on käytetävissä hakemistossa c:\ajk\tre |
|
| Tutustu TREGRAF ohjelman avulla AJKA61.TRE tietokantaa käyttäen keskeisiin pääomanmuodostuksen muuttujiin, niiden minimi- ja maksimimuutoksiin, trendeihin ja standardipoikkeamiin. | |
Paperin tuotanto o Taulukko: kiihdytin o Kiihdytinteorian matematisointi o Joustava kiihdytin
Avain pääomanmuodostuksen suuren vaihtelun ymmärtämiseen on kiihdytinperiaate.
Kiihdytinperiaatteen ydinajatus on:
Jos tuotantokapasiteetti on täyskäytössä, pääomanmuodostusta on kasvatettava tuotannon kasvuun verrattuna kiihtyvällä nopeudella.
Tarve tuotannossa tarvittavan pääomakannan kasvattamiseen eli juuri pääomanmuodostukseen kiihtyvällä nopeudella syntyy siitä yksinkertaisesta tosiasiasta, että tietyn tuotannon määrän aikaansaamiseen tarvitaan tietyn suuruinen työpanos ja tietyt koneet, laitteet ja rakennukset eli olemassa oleva pääomahyödykkeiden varanto. Pääomahyödykkeiden varannon täytyy siis olla tietyssä suhteessa tuotannon määrään. Koska pääoman muodostus on lisäystä olemassa olevaan varantoon ja vain pieni osa varannosta, sen täytyy ksvaa 'kahta kauheammin' jos varannonkin pitää kasvaa esim. 5 prosenttia sen takia, että tuotantoa on voitava kasvattaa 5 prosenttia. Tämän periaatteen on ensimmäisenä esittänyt J M Clark tutkittuaan vuosisadan alussa rautatievaunukapasiteetin kysyntää ja tarjontaa. Sama periaate voidaan esittää pelkistetyin luvuin Suomen kansantalouden ytimestä, paperiteollisuudesta kokoonkeitetyllä esimerkillä:
| Paperin tuotanto ja koneinvestoinnit |
| Suomessa oli vuonna 1989 käytössä 85 paperikonetta, joiden yhteenlaskettu tuotanto oli noin 6.8 miljoonaa tonnia. Koneiden keskimääräinen tuotanto oli siis 80 000 tonnia. Kapasiteetin käyttöaste oli vuonna 1989 korkea eli noin 94 prosenttia. Vuonna 1976 konekanta oli ollut 100 yksikköä ja niiden tuotanto 4.2 miljoonaa tonnia. Paperikone on 'melkein elävä organismi' siinä mielessä, että sitä uusitaan jatkuvasti osa osalta. Tälläkin hetkellä voi olla käytössä yli 50 vuotta vanhoja runkoja. |
Näiden paperin tuotantoa koskevien tietojen perusteella laadimme yksinkertaistetun erimerkin. Oletamme, että 1990 konekanta on 100 kappaletta ja vuosituotanto 7 miljoonaa tonnia. Lisäksi oletamme, että kapasiteetti on täyskäytössä ja että paperikoneen keski-ikä on 20 vuotta, jolloin vuotuien uusimistarve on 5 konetta. Tällä uusintainvestointien määrällä paperikonekanta pysyy entisen suuruisena ja voidaan tuottaa jatkuvasti noin 7 miljoonaa tonnia paperia. Tavanomainen 3 prosentin kysynnän kasvu merkitsee, että konekantaa on myös lisättävä noin 3 prosentilla eli 3 koneella vuodessa. Pääomanmuodostus on siis: uusintainvestoinnit 5 plus uusinvestoinnit 3 eli yhteensä 8 konetta vuodessa.
Oletaan, että vuonna 1991 kysyntä kasvaa 10 prosenttia. Koska kapasiteetti on käytännöllisesti katsoen täyskäytössä, on tuotannon lisääminen mahdollista vain hankkimalla vastaavasti uusia koneita. Vain jos konekantaa lisätään 10 koneella, pystytään kasvanut kysyntä tyydyttämään. Siis investointien on kasvettava 8 asemesta 15 koneella. Eli 10 prosentin kysynnän kasvu aiheutti kylläkin vain 10 prosentin kasvun pääoma kannassa , mutta lähes 90 prosentin kasvun pääoman muodostuksessa .
Kulutus Pääomanmuodostus, kpl Koneiden Vuosi 1000 t korvaus netto brutto kasvu% määrä 1990 7000 5 3 8 100 1991 7700 5 10 15 88 110 1992 8400 5 10 15 0 120 1993 8750 5 5 10 -33 125 1994 8750 5 0 5 -50 125 |
| T7.1 Kulutuksen vaikutus pääomanmuodostukseen |
Jos paperin kysyntä myös vuonna 1992 kasvaa 700 tonnilla eli 10 koneen vuosituotannon verran, tarvitaan taaskin 5 korvausinvestointikonetta ja 10 uusinvestointikonetta eli 15 konetta. Nyt pääoman muodostus ei edellisestä vuodesta kasvanut lainkaan, vaikka tuotanto kasvoikin, samoin pääomakanta. Siis investoinnit kasvavat vain, kun tuotannon kasvu kiihtyy. Siitä nimitys kiihdytinteoria.
Tarina jatkuu edelleen. Jos nyt 1993 kysynnän kasvu jääkin alle puoleen entisestään, eli 350 tuhanteen tonniin, siis 5 koneen vuosituotantoon, investoinnit eli pääomanmuodostus supistuu 15 koneesta 10 koneeseen. Kysynnän kasvun pysähtyminen vuonna 1994 pudottaa edelleen investointeja, koska nyt tarvitaan vain korvausinvestoinnit eli 5 konetta.
Jo Clark korosti sitä seikkaa, että kiihdytinteoria ei toimi, jos tuotantokapasiteettia on vapaana. Silloinhan tuotantoa voidaan lisätä ottamalla käyttöön jo olemassa olevaa kapasiteettia. Mitään uusinvestointeja ei tarvita. Kiihdytinperiaate on kuitenkin kansantalouden kokonaismallissa käytettävän investointiteorian lähtökohta.
Tämän, ns. naivin kiihdytinteorian matematisointi tapahtuu seuraavasti: Merkitään tuotannon määrää Q ja pääomakantaa K. Silloin pääomakerroin
k = K / Q ja K = k Q
Jos nyt tuotanto (tuotannon tarve, kysyntä) muuttuu, muuttuu pääomakannan tarve samassa suhteessa, eli
![]()
Mutta mitä on pääomakannan muutos? Mitäpä muuta kuin (netto)investoinnit eli (netto)pääomanmuodostus In. Investointien riippuvuus tuotannon muutoksesta voidaan siis kiihdytinteorian mukaan merkitä:
![]()
Tätä nimitetään naiviksi kiihdytinteoriaksi, yksinkertaisesti siitä syystä, ettei sillä pärjätä alkuunkaan, jos ryhdytään empiirisestä aineistosta selvittämään pääomanmuodostuksen riippuvuuksia. Kansantalouden kokonaistuotannon muutokset ovat käytännössä 0 ja 8 prosentin välillä. Nollakasvu edellyttäisi siis nettoinvestointien jäämistä kokonaan pois. Näin ei kuitenkaan koskaan ole tapahtunut. Pääoman muodostuksen kasvu on kyllä silloin tällöin ollut negatiivista, mutta koskaan nettoinvestoinnit eivät ole jääneet nollaksi, niin ei siis myöskään pääomakannan kasvu.
Jos kuitenkin tätä periaatetta kokeillaan empiiriseen aineistoon, kuten kansion c:\ajk\kok tiedostossa INVEST.REG on tehty, kannattaa yhtälöön liittää vakiotermi, joka silloin tulkitaan autonomiseksi eli tuotannon muutoksista riippumattomaksi pääomanmuodostukseksi.
07 Pääomanmuodostus heilahtelee o Suomen kansantalous o Kansantalouden kurssit o AJK kotisivu
Huomattavasti parempaan selitys- ja ennakointikykyyn päästään, jos käytetään joustavan kiihdyttimen periaatetta. Sen esittivät toisistaan riippumattomissa tutkimuksissaan Goodwin ja Chenery 1950-luvun alussa.
Lähtökohtana joustavan kiihdyttimen hypoteesissa on varannonsopeutusmalli , jonka mukaan
(Netto)pääomanmuodostus In tapahtuu kiinteässä suhteessa halutun pääomakannan K* ja olemassa olevan pääomakannan K1 erotukseen.
Tässä, kuten kaikkialla tässä tekstissä numero tunnisteen K1 lopussa tarkoittaa edellisen vuoden tietoa. Varannonsopeutusperiaatteen matematisointi malliksi tapahtuu seuraavasti:
In = m (K* - K1)
| Mutta mikä on tämä haluttu pääomanmuodostus?
Eihän sellaista voida mitata. Vai voidaanko? |
Kyllä vain. Mehän teimme sen jo. Haluttu pääomakanta on kiinteässä suhteessa haluttuun tuotantoon eli K* = k Q. Tästä saadaan taaskin (tarkkaan ottaen netto)pääomanmuodostus
In = m (k Q - K1)
= m k Q - m K1
Nähdään, että tuotannon määrä on mukana kuten edellä naivin kiihdyttimen tapauksessakin, mutta nyt tuotannon taso, ei sen muutos.
Siirtyminen nettopääomanmuodostuksesta eli uusinvestoinneista bruttopääomanmuodostukseen käy leikiten. Uusintainvestointien voidaan olettaa olevan poistojen suuruiset ja poistot taas tapahtuvat tietyssä suhteessa olemassa olevaan pääomakantaan. Jos poisto-osuus (= poistoprosentti/100) on d, ovat poistot (=uusintainvestoinnit)
D = d K1
Silloin bruttopääomanmuodostus on vastaavasti
Kun joustavan kiihdyttimen periaatetta ryhdytään soveltamaan käytäntöön eli suoritetaan ekonometrisia laskelmia havaintoaineistolla, ei tässä saatuja kolmea parametria ole tarpeen erottaa toisistaan. Riittää, kun laskemme parametrit b (= m k) ja c (= - m + d). Käytännön laskelmiin liitämme vielä vakiotermin, joka taaskin voidaan tulkita autonomiseksi pääomanmuodostukseksi. Tällä tavoin joustavan kiihdyttimen hypoteesin mukainen estimoitava investointifunktio on muotoa
I = a + b Q + c K1
Oleellista on, että tämä joustavan kiihdytinteorian mukainen malli antaa selvästi paremman selityksen pääomanmuodostukselle kuin naivin kiihdytinteorian mukainen malli. Selityskykyä voidaan vielä piirun verran parantaa käyttämällä yhtä 'ylimääräistä' viivettä, siis yhtälöä
I = a + b Q1 + c K2
| Osikossa puhuttiin odotuksista. Miten ne ilmenevät joustavan kiihdyttimen teoriassa? |
Olikin unohtua. Tässä kehitteillä oleva kansantalouden investointifunktiolla tarkoitetaan kuvata päätöksentekoa yrityksissä samalla tavoin kuin kulutusfunktio kuvaa kuluttajien päätöksentekoa. Kun pääomanmuodostuksesta saadaan tilastotietoja, ne ovat tietoja toteutuneesta päätöksenteosta. Niitä investointeja koskevat päätökset on tehty vuotta tai paria aikaisemmin silloin vallinneen taloudellisen tilanteen mukaan.
Näin ollen kysymyksessä on ns. tekninen viive, eli se seikka, että investointipäätösten kypsyminen valmiiksi tuotannoksi vie tietyn ajan. Ensin päätetään ryhtyä rakennusprojektiin. Sitten rakennus suunitellaan, piirretään, haetaan luvat. Koosta riippuen tämä vie aikaa vähintään viikkoja, ehkä kuukausia, joskus jopa vuosia. Sitten tehdään perustus. Sitten seinät, sitten sisustus ja lopuksi viimeistellään. Nämä vaiheet eivät näy tilastotiedoissa. Vasta kun rakennus otetaan valmiina köyttöön, se saman tien joutuu kansantulotilaston investointeihin.
Vuosi sitten vallinneita odotuksia kuvaa viimeksi kehittelemässämme investointifunktiossa silloin vallinnut taloudellinen tilanne. Viimeksi käsittelemässämme joustavan kiihdyttimen hypoteesissa odotuksia kuvaavat siis vuoden takainen eli yhdellä viivästetty tuotannon määrä ja kahdella viivästetty eli päätöshetkeä edeltäneen vuoden pääomakanta.
07 Pääomanmuodostus heilahtelee o Suomen kansantalous o Kansantalouden kurssit o AJK kotisivu
Markkinakorko o Reaalikorko o Hallinnollinen korko
Vielä ei ole virketty sanaakaan korosta tai muista pääomanmuodostuksen rahoitusmahdollisuuksiin vaikuttavista tekijöistä. Nehän ovat ainakin mikrotasolla eli yrityksessä varsin painava tekijä investointiprojektien suunnittelussa. Sitäpaitsi eräs keskeisistä makromallin ideoista, useiden kansantalouden sektoreiden tai markkinoiden samanaikainen kysynnän ja tarjonnan tasapaino on alunperin esitetty nimenomaan hyödyke-markkinoiden ja rahoitusmarkkinoiden samanaikaisen tasapainottumisen ongelmana tunnetun ja kansantaloustieteen peruskursseista tutun Hicks in ISLM mallin avulla. Siinä kaksi keskeistä muuttujaa ovat tuotannon määrä ja korko. Niiden samanaikainen tasapaino antaa kansantalouden mallin ratkaisuarvot, ne muuttujien arvot, jotka ovat sopusoinnussa keskenään.
Suomen kansantaloudessa on pitkään vallinnut tilanne, jossa korolla ei ollut sitä resursseja ohjaavaa tehtävää, jota ISLM malli kuvaa. Vasta viime vuosina tilanne Suomessa on muuttunut ja korko on saanut entistä huomattavasti tärkeämmän merkityksen yritysten investointipäätöksistä. Vasta tässä tekstissä, 16 vuotta AJKA mallin syntymisen jälkeen, on ensi kerran voitu ottaa tarkasteltavaksi pääomanmuodostuksen riippuvuus korkotasosta niin että havaintaineistosta estimoitu malli saa odotusten mukaiset parametrien etumerkit ja sekä selitysaste että t-arvot täyttävät niitä koskevat minimivaatimukset. Tästä syystä myöskään tämän tekstin taustana olevassa Suomen kansantalouden AJKA mallissa ei ole ollut eikä ole vieläkään rahoitusmarkkinalohkoa.
| Eikö siis Suomen kansantalouden mallin inves tointifunktioissa ole voitu käyttää mitään rahoi tuksen merkitystä kuvaavaa muuttujaa? |
On kyllä. Suomen Pankissa on jo 1960-luvulla tehty pioneerityö Suomen kansantalouden mallien rakentamisessa ja siinä yhteydessä kehitettiin erilaisia vaihtoehtoisia indikaattoreita, joilla kuvattiin rahoitusmarkkinoiden kireyden vaikutusta pääomanmuodostukseen.
Suomen Pankin BOF1 mallissa luoton saatavuuden mittarina käytettiin pankkien keskuspankkiluoton suhdetta pankkien luotonantoon yksityiselle sektorille. AJKA mallissa on käytetty vastaavasti keskuspankkiluoton suhdetta talletuksiin.
Jälkimmäistä voidaan perustella näkemyksellä, jonka mukaan keskuspankkiluotto ja talletukset ovat molemmat investointiluottojen lähteitä. Jos talletukset tietyn keskuspankkiluoton vallitessa kasvavat, luotonanto helpottuu. Silloin keskuspankkivelan ja talletusten suhteen numeroarvo pienenee. Jotta siis malli antaisi vastaavasti kasvavan investointien määrän, on kerroinparametrin etumerkin oltava negatiivinen. Jos taas pankit joutuvat turvautumaan keskuspankkivelkaan talletusten kasvun hidastellessa, on se merkki rahan kireydestä ja rahankireysindikaattorin numeroarvo kasvaa. Silloin negatiivinen etumerkki mallissa pienentää investointiluottoja siitä mitä ne muuten olisivat. Samoin odotetaan mittauksissa negatiivista etumerkkiä, jos rahoituksen kireyden mittarina voidaan käyttää korkoa, kuten 'normaali' teoria edellyttää.
Rahoituksen kannalta tarkasteltuna korko on rahan hinta, korvaus joka on maksettava rahan käyttöoikeudesta. Jos käytetään omaa rahaa, on korko silloinkin rahan käytön kustannus, sillä se saataisiin, jos oma raha annettaisiin markkinoiden käyttöön. Tällaista laskennallista kustannusta nimitetään vaihtoehtoiskustannukseksi .
Ennenkuin otetaan korko rahoituksen saatavuuden kuvaajaksi investointifunktioon, on tehtävä eräs tärkeä tarkennus. On erotettava toisistaan käsitteet nimelliskorko ja reaalikorko . Markkinoilla normaalisti muodostuva korko on nimelliskorko. Jos korkoa ajatellaan investointihyödykkeen rahoituksen kustannuksena, niin investointihyödykkeellä aikaansaatavan tuotannon 'normaali' hinnannousu tekee mahdolliseksi maksaa osan korkokustannuksista ikäänkuin ilmaiseksi. Vasta se osa korkokustannuksesta, jota inflaatio ei kata, on investoinnin maksettava reaalisella tuottavuudellaan. Tämä osa korosta on reaalikorko.
on nimelliskorko (markkinakorko, tässä pankkien antolainauskorko) vähennettynä inflaatioprosentilla.
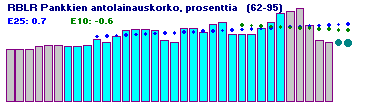 |
RBLR Pankkien antolainauskorko prosenttia BF3.4.5 ExpTrend: 62-95 1.2%, 86-95 -0.6% 62-95, Sd = 1.5 61 7.0 7.0 7.0 7.0 7.4 7.5 7.5 7.4 7.4 7.5 71 8.4 7.9 8.7 9.5 9.7 9.7 9.5 8.2 8.0 9.8 81 9.8 9.3 10.4 10.7 9.0 9.0 9.0 9.9 10.6 11.8 91 12.1 12.5 10.2 8.2 8.0 |
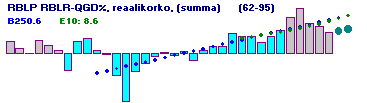 |
RBLP RBLR-QGD%, reaalikorko (summa) LinTrend: 62-95 0.2, 86-95 0.5 62-95, Sd = 4.6 61 7.0 3.1 1.3 -0.1 3.2 1.9 0.7 -4.7 3.0 3.9 71 0.8 -0.3 -5.9 -12.9 -5.0 -2.8 -0.8 0.1 -0.6 0.4 81 -2.0 0.7 1.8 1.8 5.2 4.4 4.3 2.8 4.5 6.0 91 9.6 11.8 7.8 7.0 5.4 |
| Kuviot talletettu leikepöydälle Wregajk muunnosmenusta.
Leikepöydältä kuviot on siirretty kuvankäsitteluohjelmaan, jossa ne on tallennettu HTML kielen vaatimaan .GIF muotoon. |
Suomessa aina 80 luvun puoliväliin saakka rahoitusmarkkinoilla ei näytellyt pääosaa sen enempää nimelliskorko kuin reaalikorkokaan, vaan kolmas korkokanta eli hallinnollinen korkokanta. Se on se korkokanta, joka näkyy havaintosarjana, esim. AJKA mallissa käytettynä pankkien antolainauskorkona. Hallinnollista korkokantaa ylläpidettiin hallinnollisin toimenpitein.

Oleellista on, että hallinnollinen korkokanta pidettiin normaalin kysynnän ja tarjonnan edellyttämän markkinakoron alapuolella. Tämä korko jouduttiin lainarahoituksesta maksamaan. Siinä mielessä hallinnollinen korko oli myös markkinakorko. Mutta tästäkin 'luonnollista' alemmasta korosta inflaatio maksoi täysimääräisesti osuutensa. Jäljelle jäi reaalikorko, joka nopeimman inflaation vuosina eli melkein koko 70 luvun ajan oli negatiivinen ja hyvin alhainen aina siihen saakka, kun inflaatio taintui. Tämä taas merkitsi sitä, että melkein mikä hyvänsä investointi oli riittävän tuottava rahoituksen korkokustannuksen maksamiseksi.
Tästä taas seurasi, että korko ei suorittanut tehtäväänsä resurssien allokoinnissa eli hyvien ja huonojen investointiprojektien erottamisessa toisistaan. Tämä ongelma oli ratkaistava muilla keinoilla. Alkuun rahoitus ohjautui kohteisiinsa 'hyvielokaattorin puuttellisuuden, kehittivät mittavan yritystutkimustoiminnan, jonka tehtävä oli erottaa jyvät akanoista. Jos taas korko on todellinen ja merkittävä rahoituksen kustannus se toimii myös allokaattorina, ja yritykset joutuvat itse punnitsemaan investointiprojektinsa tuottavuuden.
Ydinajatus kaikissa rahoituksen saatavuutta koskevissa hypoteeseissa on vastakkainasettelu investoinnin rajatehokkuuden ja rahoituksen rajakustannuksen välillä. Tässä on täydellinen analogia tavanomaiseen markkinahinnan määräytymiseen kysynnän ja tarjonnan vuorovaiku-tuksessa. Jos investointiprojektit asetetaan niiden tuottavuuden mukaan paremmuusjärjestykseen, saadaan korkoakselin ja investointien määrän muodostamaan koordinaatistoon alaspäin viettävä käyrä. Se vastaa kysyntäkäyrää hinta- ja määräakselien muodostamassa koordinaatistossa. Vastaavasti rahoituksen kustannukset ovat kasvava funktio rahoitettavien projektien määrän suhteen korko-määrä-akselistossa. Mitä enemmän halutaan investoida sitä riskipitoisempia projekteja joudutaan toteuttamaan ja sitä korkeampi on oltava korkokorvaus niiden rahoittajalle. Toteutuva korkotaso on se, jolla rahoituksen korko-kustannus (rahoituksen rajakustannus) on yhtä suuri kuin investoinnin korkotuotto (rajatehokkuus).
07 Pääomanmuodostus heilahtelee o Suomen kansantalous o Kansantalouden kurssit o AJK kotisivu
AJKA mallissa pääomanmuodostus on käsitelty yhtenä eränä. Näin on tehty kahdesta syystä: koko pääomanmuodostus on alle puolet yksityisen kulutuksen suuruudesta. Disaggregointi ei tuo oleellista parannusta mallin suorituskykyyn kokonaisuutena. Pantiinpa pääomanmuodostus malliin miten hyvänsä, se on ja pysyy eräänä kansantalouden mallin heikoimmista lenkeistä selityskykynsä ja ennakointikykynsä suhteen.

Periaatteessa kuitenkin pääomanmuodostus jakaantuu sitä koskevan päätöksenteon kannalta tarkasteltuna luontevasti hyvin erilaisiin komponentteihin: Asuntojen rakentaminen tyydyttää yksityistä kulutuskysyntää ja sen rahoituksessa yksityisen sektorin säästämisellä on suuri merkitys. Tuotannollinen pääomanmuodostus, muu kuin auntorakentaminen, kone- ja laiteinvestoinnit, tapahtuu yritysten toimesta ja liittyy kiinteästi tuotantotoimintaan. Tie- ja vesiraken-nusinvestoinnit ovat nekin oma lukunsa ja tapahtuvat suurimmaksi osaksi yhteiskunnan toimesta. Niiden tarkoituksena on usein tasoittaa suhdannevaihtelua, jota taas kaikki muut pääomanmuodostuksen lajit ovat ensimmäisenä aiheuttamassa.
| Kokeile tietokoneohjelmaa! | |
|---|---|
| SUOKOKZZ.exe | Pääomanmuodostuksen vaihtoehdot |
| Ohjelmapaketin tallennus kansioon c:\tmp
Kaksoisnäpäytä SUOKOKZZ Kaksoisnäpäytä SetupKOK.bat WREGAJK.EXE on käytetävissä hakemistossa
c:\ajk\kok |
|
Tutustuttuasi
nyt muutamiin pääomanmuodostusta koskeviin hypoteeseihin voit kokeilla niiden estimointia REGAJK tietokoneohjelmalla. Se lähtee liikeelle INVEST.REG tiedostosta, johon tässä käsitellyt naivin kiihdyttimen ja joustavan kiihdyttimen hypoteesien mukaiset yhtälöt on jo istutettu valmiiksi.
J.M. Clark:
Business Acceleration and the Law of Demand, Journal of Political Economy, Vol. 25, No 1 (March, 1917), pp. 217-35.
R.M. Goodwin:
"The Non-linear Accelerator and the Persistence of business Cycles", Econometrica, Vol. 19, No 1 (Jan 1951), pp. 1-17.
H.B. Chenery:
"Overcapacity and the Acceleration Principle", Econometrica, Vol 20, No 1 (Jan 1952), pp. 1-28.
Kukkonen et al.
A Quarterly Model of the Finnish Economy, Bank of Finland D:29, Helsinki 1972.
Korpela Asko
AJKA, an Econometric Model for Finland, Helsinki School of Economics A:36, Helsinki 1982.
Mallilla laaditun AJKA ennustetta laadittaessa aiheuttaa usein ongelmia investointien määräytyminen. AJKA mallin mukaan bruttopääoman-muodostus on näihin saakka määräytynyt edellä selvitetyn joustavan kiihdyttimen hypoteesin mukaisesta yhtälöstä
IFAF = - 1.8 + .72 QGF1 - .12 KFA2 t .4 6.7 4.6 RR = .945 DW = .95 SD = 3.3
IFAF = Yksityinen tuotannollinen pääomanmuodostus
QGFF = Bruttokansantuotos tuotantokustannushintaan
QGF1 = yhdellä viivästetty QGFF
KFAF = Tuotannollinen pääomakanta
KFA2 = kahdella viivästetty KFAF
TEHTÄVÄ:
Tutki joustavan kiihdyttimen teorian mukaisen yhtälön vaihtoehtoja. Sellaisina voisivat tulla kysymykseen esim
IFAF = a2 + b2 QGFF + c2 KFA1 + d2 RBR1
IFAF = a3 + b3 QGFF + c3 KFA1 + d3 KFA2
KFA1 = Yhdellä viivästetty pääomakanta
RBR1 = Luotonannon viivästetty reaalikorko
RBR1 saadaan kun nimelliskorosta RBLR vähennetään inflaatioprosentti ja sen jälkeen viivästetään. Inflaatioprosenttina voidaan käyttää bruttokansantuotoksen hintaindeksin QGDP vuosimuutosprosenttia.
Estimoi nämä funktiot ja arvioi niiden hyvyyttä
a) tilastollisten tunnuslukujen
b) talousteoreettisten näkökohtien
valossa nyt käytössä olevaan joustavan kiihdyttimen hypoteesin mukaiseen versioon verrattuna.
Tulkitse yhtälöt sanallisesti eli selvitä mitä talousteoriaa ne sisältävät.
Miten muuten kuin tilastollisten tunnuslukujen ja talousteoreettisten näkökohtien valossa olisi arvioitava yhtälön hyvyyttä?
07
sivun alkuun o H07 Harjoitustehtävät
AJK kotisivu o AJK
ohjelmasivu o Kansantalouden kurssit
o Suomen kansantalous
Asko Korpela 971103 (970306) o Asko.Korpela@kolumbus.fi (palaute)
[ccc]