2 Kansantalouden malli

1 Mallin rakenne ja teoria
2 Tasapainoratkaisu
3 Komparatiivinen statiikka
4 Menetelmän ydin
#H02 Kansantalouden malli

Tässa luvussa tarkastellaan Hicksin ISLM mallin komparatiivista statiikkaa.

AJK kotisivu o AJK opetus o Optimointi ja dynamiikka o Palaute: Asko.Korpela@kolumbus.fi (palaute AJKlle)

2.1 Mallin rakenne ja teoria

Hicks J.R.:

"Mr Keynes and the 'Classics': A Suggested Interpretation."
Econometrica, Apr 1937, pp. 14759.

Hyödykemarkkinat:

I = I(i) I' < 0 Pääomanmuodostus
S = S(Y,i) 0 < S_Y < 1, S_i > 0 Säästäminen
M = M(Y) 0 < M' < 1 Tuonti
X = X₀ Vienti

Rahamarkkinat:

M_d = L(Y,i) L_Y > 0, L_i < 0 Rahan kysyntä
M_s = M_s0 Rahan tarjonta

Tasapaino:
I + X = S + M
M_d = M_s

Sijoittamalla rakennemuodon yhtälöt tasapainoehtoihin saadaan mallin redusoitu muoto.

I = I(i) I' < 0
S = S(Y,i) 0 < S_Y < 1, S_i > 0
M = M(Y) 0 < M' < 1
X = X₀
M_d = L(Y,i) L_Y > 0, L_i < 0
M_s = M_s0

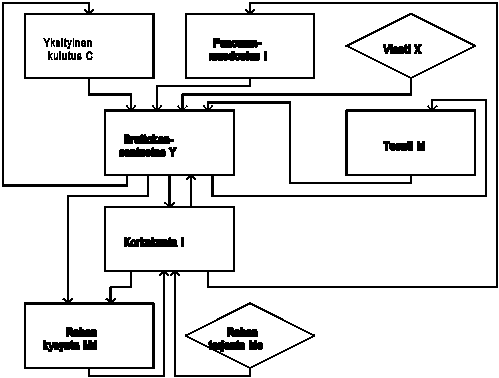
#2 Kansantalouden malli
#2.1 Mallin rakenne ja teoria
#Hyödykemarkkinat: o #Rahamarkkinat: o #Tasapaino:

2.2 Tasapainoratkaisu

Ratkaisu: Endo = f(Ekso,Para)

Yleinen funktiomuoto

Y = (X₀ ,M_s0)
i = (X₀ ,M_s0)

Komparatiivinen statiikka

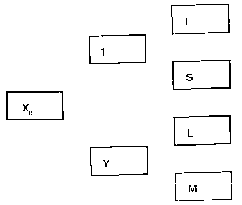
Kuviossa K2.2 on esitetty viennin X₀ suorat ja epäsuorat vaikutukset. Viennillä on S ja L funktioihin kaksi vaikutusta, vaikutus sekä koron että tulojen kautta.

Samalla tavoin voitaisiin esittää myös rahan tarjonnan M_s0 vaikutukset.

Implisiittifunktiokäsittelyä varten ISLM malli voidaan kirjoittaa myös muotoon

#2 Kansantalouden malli o #2.2 Tasapainoratkaisu o #Yleinen funktiomuoto

2.3 Komparatiivinen statiikka

#2 Kansantalouden malli
#2.3.1 Kokonaisderivaatta o #2.3.2 ISLM mallin kokonaisdifferentiaali

       Suorat Derivaatta 
KAIKKI                   MUUTOKSET 
     Epäsuorat Ketjusääntö

2.3.1 Kokonaisderivaatta

Tapaus 1: kokonaisdifferentiaali

jaetaan differentiaalilla dx₁, jolloin saadaan kokonaisderivaatta (ketjusääntö)

Tapaus 2: x₁ ja x₂ riippuvat kolmannesta w

Esim: tuotantofunktio ja aika

Tapaus 3: x₁ ja x₂ riippuvat kahdesta muusta u ja v

osittainen kokonaisderivaatta

#2 Kansantalouden malli
#2.3 Komparatiivinen statiikka
#2.3.1 Kokonaisderivaatta o #2.3.2 ISLM mallin kokonaisdifferentiaali

2.3.2 ISLM mallin kokonaisdifferentiaali

Palaamme ISLM malliin (8.38').

Muodostamme siitä kaikki osittaisderivaatat muuttujien Y ja i suhteen

ja niistä edelleen Jacobin determinantin (ks C37.6, pp 1846). Saamme

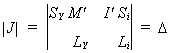
Emme voi ratkaista lausekkeesta (8.38') eksplisiittisesti tai , implisiittinen ratkaisu on

mutta voimme kirjoittaa sen tasapainon lähellä muotoon

Olettamalla differentiaali rahan tarjonnan dM_s0 suhteen nollaksi, vienti X₀ on ainoa muutoksia aiheuttava tekijä. Muodostetaan lausekkeesta (8.38') kokonaisdifferentiaali viennin X vaikutusten selvittämiseksi.

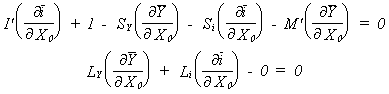
Tuntemattomia ovat nyt siis viennin muutoksesta johtuvat kansantulon ja koron muutokset eli osittaisderivaatat ja Näistä tuntemattomista, niiden kertoimista ja yhtälöihin mahdollisesti muodostuvista vakioista muodostuu kahden yhtälön ryhmä, josta tuntemattomat voidaan ratkaista

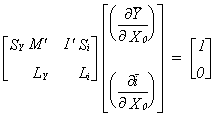
Derivaatat S_Y, M' ja L_Y pisteessä Y = Y
S_i, I' ja L_i i = i

Tässä ei merkitystä, missä pisteessä, koska funktiot ovat lineaarisia.

#2 Kansantalouden malli
#2.3 Komparatiivinen statiikka
#2.3.1 Kokonaisderivaatta o #2.3.2 ISLM mallin kokonaisdifferentiaali

Ekskursio matriisialgebraan 3 ed. pp 54124

(4.17) Ax = d
(4.18) x = A¹ d

Cramerin sääntö 3 ed. pp 107110

D = - L_i (S_Y + M') L_Y (I' - S_i)

D > 0, koska L_i < 0 L_Y > 0

S_Y > 0 S_i > 0

M' > 0 I' < 0

1. termi > 0, 2. termi > 0

Viennin vaikutukset
= kaksi komparatiivisstaattista derivaattaa

Johtopäätökset:

1. Kansantulo kasvaa, kun vienti kasvaa.

2. Korko nousee, kun vienti kasvaa.

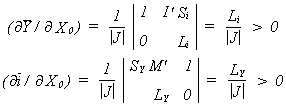
on vientimultiplier, viennin sysäysvaste

Ketjusäännön avulla voidaan selvittää myös esim. viennin vaikutus tuontiin. Ensin viennin vaikutus kansantuloon, sitten kansantulon vaikutus tuontiin.

Vienti kasvattaa tuontia, koska d/dY > 0

Samoin viennin vaikutus investointeihin

säästämiseen

Samalla tavoin saadaan kaikki rahan tarjonnan vaikutukset.

#2 Kansantalouden malli
#2.3 Komparatiivinen statiikka o #2.3.1 Kokonaisderivaatta o #2.3.2 ISLM mallin kokonaisdifferentiaali
#Ekskursio matriisialgebraan o #Cramerin sääntö
#Johtopäätökset:

2.4 Menetelmän ydin

1. Sijoita yhtälöt tasapainoehtoon.

2. Muodosta kokonaisdifferentiaali.

3. Ratkaise tarvittavat komparatiivisstaattiset derivaatat.

4. Suorita kvalitatiivinen arviointi ottaen huomioon teorian mukaiset etumerkkien (ja suuruuden) rajoitukset.

#2 Kansantalouden malli

H02 Kansantalouden malli

1. Selvitä sivulla 1 esitetyn Hicksin mallin komparatiivisstaattiset derivaatat ja , siis rahapolitiikan vaikutukset. Mihin suuntaan muutokset vaikuttavat?

2. Oletetaan, että sivun 1 mallissa osittaisderivaatan L_i rajoitus muuttuu: #Vihje:

< 0, kun i > 2 %
L_i
6 4, kun i 6 2%⁺

a) Miten tulkitset talousteorian kannalta tapauksen

L_i --> oo, kun i --> 2%⁺

b) Selvitä uudelleen osittaisderivaattojen ja arvot uusien rajoitusten vallitessa.

Vihje:

Kun L_i esiintyy sekä osoittajassa että nimittäjässä (D), osamäärä on ensin 'muokattava' muotoon, jossa se esiintyy vain jommassa kummassa. Miksi?

3. Oletetaan redusoitu kansantalouden malli

a) Mikä tässä on rahan kokonaiskysyntä M_d?

b) Analysoi tämän mallin komparatiivista statiikkaa, jos rahan tarjonta (= rahapolitiikka) muuttuu ja julkinen kulutus (= finanssipolitiikka) muuttuu.

2 Kansantalouden malli
2.1 Mallin rakenne ja teoria o 2.2 Tasapainoratkaisu
2.3 Komparatiivinen statiikka o 2.4 Menetelmän ydin
H02 Kansantalouden malli

AJK kotisivu o AJK opetus o Optimointi ja dynamiikka

Asko Korpela, kansantaloustieteen lehtori, Helsingin kauppakorkeakoulu

Asko.Korpela@kolumbus.fi (palaute AJKlle)

Asko Korpela 961129 (960929)

[ccc]