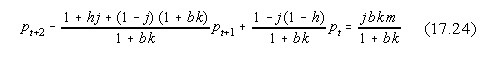
Tällä sivulla on käyty [ccc] kertaa
Malli
1. Selvitä
välivaiheet yhtälöstä (17.23) yhtälöön
2. Osoita, että
jos tässä luvussa käytety malli
3. Tässä
luvussa tarkasteltujen muuttujien p ja U
4. Pidetään
yhtälöt (17.18) ja (17.19)
a) Johda uusi
differenssiyhtälö muuttujalle p.
b) Antaako uusi
differenssiyhtälö erilaisen
c) Oletetaan j =
h = 1. Johda ehdot, joilla
d) Oletetaan j =
h = 1. Kuvaile muuttujan p
pt = a - T - b Ut + h p*t
(0 < h 1) (17.18)
p*t+1 - p*t = j (pt - p*t)
(0 < j 1) (17.19)
Ut+1 - Ut = - k (m - pt+1) (k >
0) (17.20)
1. Selvitä välivaiheet yhtälöstä (17.23) yhtälöön (17.24).
Vastaus:
(1 + b k) pt+1 - [1 - j (1 - h)] pt + j b Ut = b k m + j (a - T) (17.23)
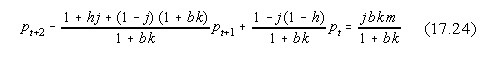
a) Siirretään aikaindeksiä yhtälössä (17.23)
![]()
b) Vähennetään tästä (17.23)
![]()
c) Tähän sijoitetaan (17.20) ja saadaan
![]()
d) Jaetaan lausekkeella (1 + bk) ja lopputulos on (17.24)
2. Osoita, että jos tässä luvussa käytety malli pelkistetään differenssiyhtälöksi muuttujan p* suhteen, tulos on sama kuin (17.24) paitsi että muuttujan p paikalla on muuttuja p*.
Vastaus:
Sijoitetaan (17.18) lausekkeeseen (17.19) ja kootaan termit
![]()
Tämän differenssioiminen antaa
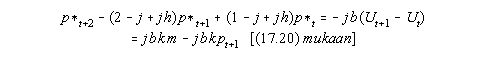
Eteenpäin siirretty versio lausekkeesta (17.19) antaa
![]()
Käytetään tätä ja eliminoidaan pt+1 termi edellisestä lausekkeesta
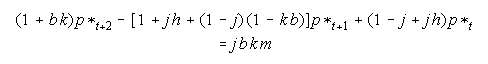
Kun tämä normalisoidaan, saadaan sama differenssiyhtälö kuin lausekkeessa (17.24)
3. Tässä luvussa tarkasteltujen muuttujien p ja U aikaurien on havaittu olevan konsistentisti suppenevia. Voiko räjähtävä aikaura olla seurauksena, jos luovutaan olettamuksesta h 1? Jos näin on, mitkä mahdollisuudet tapauksissa C1, C2 ja C3 voivat tulla kysymykseen?
Vastaus:
Olkoon h > 1. Silloin (17.26) ja (17.27) mukaan vieläkin pätee ehto b1 + b2 > 0 ja (1 - b1)(1 - b2) > 0. Mutta lausekkeessa (17.26') b1 b2 voi nyt olla suurempi kuin yksi. Tästä seuraisivat tapaukset 1D, 2D ja 3D, joissa kaikissa on räjähtävä aikaura.
4. Pidetään yhtälöt (17.18) ja (17.19) muuttumattomina, mutta muutetaan yhtälöä (17.20) siten että se on
Ut+1 - Ut = - k (m - pt)
a) Johda uusi differenssiyhtälö muuttujalle p.
b) Antaako uusi differenssiyhtälö erilaisen tasapainoarvon ?
c) Oletetaan j = h = 1. Johda ehdot, joilla karakteristiset juuret jakautuvat tapauksiin C1, C2 ja C3.
d) Oletetaan j = h = 1. Kuvaile muuttujan p aikauraa (suppenemista ja räjähdystä), kun b k = 3, 4 ja 5.
Vastaukset:
a) Johda uusi differenssiyhtälö muuttujalle p.
Vastaus:
pt+1 - pt = - b (Ut+1 - Ut) + h (p*t+1 - p*t)
= b k (m - pt+1) + h j (pt - p*t) (17.21)
Lausekkeen (17.21) ensimmäinen rivi pitää yhä paikkansa, mutta toinen rivi on nyt
![]()
Vastaavasti (17.23)
(1 + b k) pt+1 - [1 - j (1 - h)] pt + j b Ut = b k m + j (a - T) (17.23)
saa muodon
![]()
Ja (17.24)
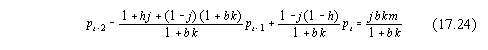
saa muodon
![]()
b) Antaako uusi differenssiyhtälö erilaisen tasapainoarvon ?
Vastaus:
Ei, yhä pätee pviiva = m.
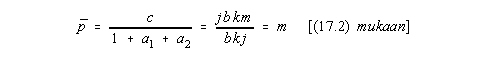
Samoin kuin jatkuvan ajan tapauksessakin, inflaation tasapainoarvo on yhtä kuin rahaekspansion nopeus.
c) Oletetaan j = h = 1. Johda ehdot, joilla karakteristiset juuret jakautuvat tapauksiin C1, C2 ja C3.
Vastaus:
Olettaen j = h = 1 saamme a1 = b k - 2 ja a2 = 1. Silloin
a12 <=> 4 a2 joss (b k - 2)2 <=> 4 joss b k <=> 4
Tulo b k erottaa kolme tapausta toisistaan.
d) Oletetaan j = h = 1. Kuvaile muuttujan p aikauraa (suppenemista ja räjähdystä), kun b k = 3, 4 ja 5.
Vastaus:
Jos b k = 3,
juuret ovat kompleksiset ja ![]()
aikaura aaltoilee suppenematta (ja räjähtämättä).
Jos b k = 4,
kertautuva reaalijuuri b = - 1/2 (4 - 2) = -1
aikaura heilahtelee tasapainon ympärillä suppenematta.
Jos b k = 5,
erisuuret reaalijuuret b1, b2 =
1/2 (- 3 ± ![]() )
= -0.38, -2.62
)
= -0.38, -2.62
dominoivan juuren itseisarvo suurempi kuin yksi: aikaura heilahtelee tasapainon ympärillä räjähtäen.
OptDyn kotisivu o AJK kotisivu
Asko Korpela, kansantaloustieteen lehtori, Helsingin kauppakorkeakoulu
Asko.Korpela@kolumbus.fi (palaute AJKlle)
Asko Korpela 971125 (971125)